Bipolar disorder is a mental health problem that primarily affects mood. Symptoms of bipolar disorder are extreme irritability or agitation, a period of feeling empty, loss of interest in usual activities, sleep problems Etc. Symptomatic recovery is a dimensional measure that refers to improvement in the magnitude of symptoms. This investigation aims to determine the association between the burden of symptoms and time to symptomatic recovery of bipolar disorder that may increase more awareness about this disorder.

A Bayesian joint modeling of longitudinal and survival data was proposed to examine the association between the burden of symptoms and time to symptomatic recovery of bipolar disordered individuals at Jimma University Medical Center, Jimma, Ethiopia. The data in this investigation were retrospective longitudinal data and survival data from all the admitted follow-up of bipolar disorder patients from September 2018 to January 2020.

From the total of 257 bipolar disorders, about 116(45.1%) of them experienced an event of recovery. The time interval of follow up, age, the interaction between time interval of follow up and adolescent first onset of the disease, the interaction between time interval of follow up and event of relapse, the interaction between linear time interval of follow up and existence of other cofactors, and the interaction of substance abuse and chewing khat have significantly affected the log expected burden of bipolar symptoms. In survival sub-models, the covariates; divorced, event of relapse, mixed type of episodes significantly affect the time to symptomatic recovery at 95% confidence level. The association between burden of bipolar symptoms and time-to- symptomatic recovery is explained by α₀ = - 8.403 with a [- 11.157,- 6.576]. It associates longitudinal count, the burden of symptoms, and time-to-symptomatic recovery of bipolar disorder using shared random effect parameters. There was a significant negative relationship between the subject-specific random intercept (baseline) of the burden of symptoms and the time to symptomatic recovery of bipolar disorder. Their 95% credible intervals exclude zero.

This study using the Bayesian joint modeling of longitudinal and survival has revealed a strong negative relationship between the event of recovery and the burden of bipolar symptoms at the baseline time. The study indicates that at the beginning, since the burden of bipolar symptoms is high, the chance of symptomatic recovery is low. And, we hypothesize that individuals with a higher initial symptom burden or a slower rate of symptom reduction (captured by b_i) will experience a longer time to recovery. So, bipolar disorders at the initial follow-up need exceptional service and treatment.

Bipolar disorder is a persistent, psychiatric severe illness with an estimated prevalence of approximately 1%, while its lifetime prevalence is about 3% worldwide [1, 2]. Bipolar disorder, also known as manic-depressive disorder, is a mental illness problem that primarily affects mood. Symptoms of bipolar disorder are extreme irritability or agitation, a period of feeling empty, loss of interest in everyday activities, sleep problems etc. Bipolar disorder affects over five million people in the United States [3]. Bipolar episodes are a drastic change in behavior and mood and range from joyful and overexcited (manic episodes) to deplorable and hopeless (depressive). These disorders have different episodes, such as manic episodes, hypomanic episodes, depressive episodes, and mixed episodes. Causes of bipolar disorders include childhood trauma, stressful life events, Self-esteem problems, and genetic inheritance [4]. In most developing countries, particularly in sub-Saharan Africa, mental health care resources are scarce Stanley [5], and the delay in seeking treatment for bipolar disorder is extended [6]. In sub-Saharan Africa, unipolar depression was the third leading cause of disease burden by 2020 and it is expected to become the second leading cause of disease burden worldwide [7].

The overall prevalence of mental illness in South Africa was about 25% among adults [8]. Moreover, mental health problems account for 12.45% of the burden of diseases in Ethiopia, and 12% of the Ethiopian people are suffering from some form of mental health problems, of which 2% are severe cases [9]. Similarly, in 2005, the projected lost days of work to the Ethiopian society was estimated to be 112.8 million, 140 assuming a 2.9 per cent lifetime prevalence rate of bipolar disorder in the general population and 93.52 cumulative lost days of work from each patient annually [10].

Mental distress is relatively common in Jimma town. The decentralization of mental health services and their integration with primary health care and community health agents in creating awareness among the community members is recommended [11]. Symptomatic recovery is a dimensional measure that refers to improvement in the magnitude of symptoms. Recovery should not be defined merely by symptomatic remission or even syndrome remission; instead, recovery should include symptomatic recovery, syndrome recovery, functional recovery, and a return to an acceptable quality of life for the patient [12]. Longitudinal and survival data analysis are among the fastest expanding areas of statistics and biostatistics in the past three decades. The critical issues for longitudinal data analysis are how to account for the within-subject correlations and handle missing observations. On the other hand, survival analysis deals with survival data or time-to-event data where the outcome variable is time to event [13]. Joint modeling of longitudinal and survival time is an affluent and active research area examining the association between longitudinal and survival processes. It also enhances longitudinal modeling by allowing for the inclusion of non-ignorable dropout mechanisms through survival tools and survival modeling with internal time-dependent covariates [14]. Joint modeling of longitudinal and survival time were primarily used to adjust for no ignorable missing data due to informative or outcome related dropouts, which we cannot appropriately handle using linear mixed and generalized linear mixed-effects models [15]. Joint modeling improves efficiency and reduces bias when the two outcomes of interest are correlated [15, 16], improving prediction and application to outcome surrogacy [17].

Nevertheless, to the best of my knowledge, there is virtually no advanced literature using the joint models on bipolar disorder that leads to an unknown association between burdens of bipolar and duration of recovery, except the studies about the prevalence of bipolar in Ethiopia based on cross-sectional data. Even though some documents were there, they used multiple linear and logistic regression or separate models survival and longitudinal to identify determinant factors and assess risk factors over time separately without raising the association between burden of bipolar symptoms and time to symptomatic recovery using the survival and longitudinal joint model [18,19,20].

Studying the association between the burden of bipolar symptoms and time to recovery is one way of overcoming the mental health problem in the community by addressing the effects of the burden of bipolar symptoms on the duration of recovery and significant factors of the burden of bipolar symptoms. This study may help physicians and researchers as a benchmark when investigating related studies. It also gives a chance to examine the progression and change trajectory of burden bipolar symptoms and its recovery duration. Awareness of this will allow all the concerned body to take appropriate measures to reduce the burden of bipolar symptoms and reduce the risk factor or covariates.

This study aims to determine the association between the burden of symptoms and time to symptomatic recovery of bipolar disorder using Bayesian joint modeling of longitudinal and survival time that may increase more awareness about this disorder.

This study is conducted in the Jimma University Medical Center, located in Jimma Zone, Oromia Regional State, and southwest Ethiopia. Jimma zone is located at a distance of 325 km from Addis Ababa, the center of the Ethiopian country. The hospital currently employs almost 1,000 people and each year provides tertiary care services for approximately 9,632 inpatients, 5,000 accident and emergency cases, and 80,000 outpatients from a catchment area population of 15 million. The psychiatry inpatient unit has 24 beds, which are mainly used to manage acutely ill patients (www.hindawi.com/journals/psychiatry/2020/8739546/).

In this study, data from retrospective cohort admitted follow up of all bipolar disorder patients, who have followed at least three visits from first, September 2018 to first January 2020 in Jimma University Medical Center is included. The longitudinal and survival data are extracted from the patient's card which contains epidemiological, laboratory, and clinical information of all bipolar disorder patients after identifying patients admitted and follow-up. Data was carefully extracted from secondary sources using well-trained data collectors in the Jimma University Medical Center.

Inclusion criteria

All persons registered with complete information, including study variables of interest in the chart, were considered eligible for the study. The patients were to be included in the study, and they must take treatment at least one time from the hospital.

Exclusion criteria

The patients with insufficient information regarding study variables on the registration card were not eligible. Thus, the patients lost from the study without starting any treatment were omitted.

Dependent variables

The response variables of this study are two;"Burden of bipolar symptoms", which counts the number of bipolar symptoms the patient shows a medical psychiatrist repeatedly records at every follow-up time. At every follow-up time, the psychiatrists ask the bipolar disorder also the caregivers about the patient's symptoms and record on the patient's card (book). Moreover, it is a counting variable. The other response is"Time to symptomatic recovery of bipolar disorder", which is the length of time in a month to get recovery. It is recorded on patients'cards when all symptoms are improved or removed.

Independent variables

The variables used in this study are Age, sex, the event of relapse, First onset, Bipolar type, educational status, Other cofactors, Marital status, Types of episodes, Family history of the disease, Substance abuse, Religion, Time interval of the follow up.

Descriptive statistics

The study considers both descriptive and inferential statistics. Descriptive data analysis was used to look at data patterns. Whether the final model fit the data yields fitted values that resemble the data and capture the main features of the data. Exploratory analysis of longitudinal data seeks to discover patterns of systematic variation across groups of patients and aspects of random variation that distinguish individual patients [21]. Kaplan Meier plot (s) and table of frequency was used to summarize the information of bipolar used to summarize disorders recorded from the patient's chart (card).

Generalized Linear Mixed Models (GLMMs)

To address the complexities of analyzing correlated and non-normal data, we employ a Generalized Linear Mixed Model (GLMM). GLMMs extend the framework of generalized linear models by incorporating random effects, allowing for the modeling of data exhibiting within-subject correlation or clustering [22, 23]. They can model over dispersion and correlation by incorporating the random effect [24]. The response variable, denoted as y_i(\({t}_{j}\)), represents the outcome for the \({{t}_{j}}^{th}\) observation within the i^th individual, with observations assumed independent conditional on the random effects. The relationship between the response and predictor variables is modeled through a linear predictor, \({\eta }_{i}({t}_{j})= {{X}_{i}({t}_{j})}^{T}\beta +{{Z}_{i}({t}_{j})}^{T}{b}_{i}\) where \({X}_{i}({t}_{j})\) represents fixed-effects covariates, β represents the associated fixed-effects coefficients, \({Z}_{i}({t}_{j})\) are the random-effects covariates, and b_i represents the random effects for the i^th individual. These random effects are typically assumed to follow a multivariate normal distribution with mean zero and covariance matrix D, i.e.,\({b}_{i}\sim MVN\left(0,D\right)\). A link function,\(g\left({\mu }_{i}({t}_{j})\right)={\eta }_{i}({t}_{j})\), connects the linear predictor to the conditional mean of the response,\({\mu }_{i}({t}_{j})=E({y}_{i}({t}_{j})/{b}_{i})\).The conditional distribution of \({y}_{i}({t}_{j})/{b}_{i}\) is assumed to belong to the exponential family, accommodating various data types, including normal, binomial, Poisson, gamma, and negative binomial.

A longitudinal Poisson mixed model is a type of generalized linear mixed-effects model (GLMM) specifically designed for analyzing count data collected repeatedly over time on the same subjects [22, 23]. It extends the standard Poisson regression model by incorporating random effects to account for within- subject correlation in the repeated measurements. Let \({y}_{i}({t}_{j})\) denote the count outcome for subject i at time t_j, where i = 1,2,…..n and j = 1,2,…. n_i. We assume that \({y}_{i}({t}_{j})\) follows a Poisson distribution, conditional on a subject specific random effect b_i. The probability mass function (PMF) of the Poisson distribution is given by:

where \({\lambda }_{ij}\) is the conditional mean parameter, representing the expected count for subject i at time.

t_j. In GLMMs, a link function is used to relate this mean to a linear combination of predictors [9, 10]. A common goal is to model the logarithm of the mean as a linear function of fixed and random effects. To achieve this, we take the logarithm of the conditional mean:

where \({\eta }_{ij}\) is the linear predictor, which is a linear combination of fixed and random effects;

Therefore, the log link function is defined as:

This equation directly models the logarithm of the conditional mean \({\lambda }_{ij}\) as a linear combination of fixed effects \({{X}_{i}({t}_{j})}^{T}\beta\) and random effects \({{Z}_{i}({t}_{j})}^{T}{b}_{i}\). Taking the exponential of both sides gives the mean parameter:

where; \({X}_{i}\left({t}_{j}\right)\) is the design vector for the fixed effects at time tj for subject I, β is the vector of fixed-effects regression coefficients, \({Z}_{i}\left({t}_{j}\right)\) is the design vector for the random effects at time tj for subject i, bi is the vector of random effects for subject i. It is assumed to follow a multivariate normal distribution with mean 0 and variance–covariance matrix D:

The random effects \({b}_{i}\) account for the within-subject correlation, meaning that observations from the same subject are more similar than observations from different subjects. The variance–covariance matrix D, specifies the structure of this correlation.

Parameter estimation in the longitudinal Poisson mixed model relies on maximizing the likelihood function. This involves integrating out the random effects, leading to a likelihood function of the form:

where; y is the matrix of all observed outcomes \((y={y}_{i}\left(t\right))\) and f(bi; 0;D) is the probability density function of the multivariate normal distribution with mean 0 and variance–covariance matrix D. The integral in the likelihood function is often intractable and requires numerical approximation methods for parameter estimation. such as: Penalized Quasi-Likelihood (PQL) which is an approximate method that linearizes the model [24], Gaussian Quadrature (AGQ which is a more accurate numerical integration technique [25] and Markov Chain Monte Carlo (MCMC) which is a Bayesian method that uses simulation to approximate the posterior distribution of the parameters [26]. In this study Penalized quasi-likelihood approximation was used to estimate the GLMM. The glmmPQL() function works by repeated calls to lme in the R package uses the Laplace approximation to do GLMM regression as the default method that the package nlme had loaded at first.

Survival data analysis

Survival analysis or time-to-event data analysis refers to statistical methods for time-to-event data. Censoring occurs when we have some information about individual survival time, but we do not know the survival time exactly; there are many types of censoring, including right-censoring, left-censoring, interval censoring, and double censoring [27].

The Cox proportional hazards model, introduced by Cox [28], is a semi-parametric approach to survival analysis. It makes no assumptions regarding the functional form of the baseline survival function, S₀(t) the non-parametric component, but assumes a parametric relationship between the covariates and the hazard function. This feature gives rise to the term"semi-parametric."The survival function for an individual with covariate vector X is modeled as:

where: \(S\left( t|X\right)\) is the survival probability at time t for an individual with covariate vector X. S₀(t) is the baseline survival function. X is the vector of covariates. Β is the vector of regression coefficients representing the log hazard ratios. Despite the unspecified form of S₀(t), the model enables the estimation of regression coefficients, hazard ratios, and adjusted survival curves. Cox demonstrated that the estimation of β can be based on the partial log-likelihood function [28];

where: \(pl\left(\beta \right)\) is the partial log-likelihood function; n is the number of individuals in the dataset; \({\delta }_{i}\) is an indicator variable equal to 1 if individual i experienced the event and 0 if censored; X_i is the vector of covariates for individual i; T_i is the observed time (either event time or censoring time) for individual i. The summation inside the logarithm is over all individuals j who are at risk at time T_i (i.e., those who have not yet experienced the event or been censored).

The longitudinal and survival joint modeling

The joint analysis is an elegant approach to model the association between time-dependent covariates and the event of interest when the covariate trajectory is not entirely observed and subject to measurement error and biological variation [29]. When primary interest is in the association between such endogenous time-dependent covariates and survival, an alternative modeling framework has been introduced in the literature, known as the joint modeling framework for longitudinal and time-to-event data [30]. To fit the Bayesian joint longitudinal and survival model using the JMbayes R package, first separately a generalized linear mixed model for the longitudinal data and a Cox-PH model for the survival data has been fitted.

We consider a longitudinal sub-model for count data, specifically a Poisson mixed-effects model. Let yi(t) denote the observed count for subject i at time t. We assume that conditional on the random effects bi, yi(t) follows a Poisson distribution.

The conditional mean \({\lambda }_{ij}\) is modeled using a log link function:

where Xi(t) and Zi(t) are the design vectors for the fixed effects β and random effects bi, respectively. The random effects are assumed to follow a multivariate normal distribution:

where D is the variance covariance matrix. This model captures the within subject correlation of the longitudinal counts and allows for individual deviations from the population average trajectory. The Poisson distribution assumes that the counts are independent and identically distributed, conditional on the random effects. Over dispersion (variance greater than the mean) can be addressed using a negative binomial distribution instead of the Poisson [31].

The survival sub-model is a Cox proportional hazards model [25], which relates the hazard rate to the longitudinal marker. Let T_i be the event time for subject i, and δi be the event indicator (1 for event, 0 for censored. The hazard function is given by:

where \({h}_{0}\left(t\right)\) is the baseline hazard function, X_i is a vector of baseline covariates, \(\gamma\) is the corresponding vector of regression coefficients, α quantifies the effect of the longitudinal outcome m_i(t) on the hazard or it is the association parameter that quantifies the relationship between the longitudinal process and the hazard and m_i(t) is the true unobserved longitudinal value at time t. where; \({m}_{i}(t)={m}_{i}(s),\) 0 < S < t. Since m_i(t) is unobserved, we replace it with the predicted value from the longitudinal sub-model,

In particular, we obtain that using the known relation between the survival and cumulative hazard functions:-

This implies that the corresponding survival function depends on the whole covariate history m_i(t). However, within the joint modeling framework, it turns out that following such a route may lead to an underestimation of the standard errors of the parameter estimate [30]. To avoid such problems, we explicitly defined h₀(.). For instance, step-functions and linear splines used a B splines approximation to obtain a non-parametric estimate of the risk function [30], used restricted cubic splines. Two simple options that often work pretty satisfactorily in practice are the piecewise-constant and regression splines approach.

Shared parameters in the longitudinal and survival bayesian joint model

The joint model connects the longitudinal and survival processes through the random effects b_i [32]. These shared random effects induce correlation between the longitudinal measurements and the time to event. When bi is used to link together y_i and T_i, the approach is referred to as shared parameter models, although bi is a covariate, not a parameter, in the model for time T_i. A more general extension of shared parameter a latent zero-mean bivariate Gaussian process U_i(t) = (U_1i(t),U_2i(t)) [33] is used to characterize the association between Y and T. In particular, the model is given by; g(E(µ_y)) = X_iβ₁^T + U_1i(t_ij) and λ_i(t|U₂) = h₀(t)exp (X_i β₂ + U_2i(t_ij)) Various functional forms have been proposed for the latent processes U_1i(t) and U_2i(t)). For example, U_1i(t) can be b_0i or b_0i + b_1i and etc. where b_0i and b_1i are random intercept and slope, respectively, and U_2i(t)) can be γU_1i(t), γ₀b_0i + γ1b_1i + γ2U_1i(t).

Bayesian estimation of longitudinal and survival joint model

The joint model likelihood is formed by assuming conditional independence between the longitudinal and survival processes, given the shared random effects. The likelihood for subject i is.

the product of the likelihoods for the longitudinal and survival components:

where: θ is the vector of all model parameters (β, D, γ, α, parameters in h₀(t)). \(p\left({y}_{i}\left(t\right)|{b}_{i},\beta \right)\) is the probability mass function of the Poisson distribution for the longitudinal counts. \({S}_{i}(t/{M}_{i}(t),{X}_{i})\) is the survival function, \({h}_{i}\left(t/{m}_{i},{X}_{i}\right)\) is the hazard function evaluated at the event time and \(p\left({b}_{i};D\right)\) is the probability density function of the multivariate normal distribution for the random effects.

The overall likelihood is the product of the individual likelihoods:

This product represents the likelihood of the entire dataset, assuming independence between subjects.

Compared to likelihood approaches, Bayesian methods in principle are relatively straightforward to implement that the expectation is computed numerically through Monte Carlo simulations by repeatedly drawing random (θ,b_i) samples from its posterior via Gibbs or Metropolis Hastings samplers. In the Bayesian framework, we don't just maximize the likelihood; we combine it with our prior beliefs about the parameters. This prior information, represented by the prior distribution π(θ), influences our final estimates. The posterior distribution \(\pi \left(\theta ,b|{D}_{n}\right)\), reflects our updated beliefs about the parameters after observing the data and is proportional to the product of the likelihood and the prior distributions:

where; \(L\left(\theta \right)\) is the overall likelihood, representing the data's contribution to our knowledge \(\text{p}(\text{b}/\uptheta )\) Specifies the distribution of the random effects, usually a multivariate normal with mean zero and covariance matrix D. This models the heterogeneity between subjects. \(\uppi (\uptheta )\); represents the prior.

distribution over all the model parameters θ [34, 35]. This allows us to incorporate existing knowledge or reasonable constraints on the parameter values. Where \({D}_{n}={\left\{{y}_{i},{t}_{i},{T}_{i},{\delta }_{i},{X}_{i}\right\}}_{i=1}^{n}\) represents the entire observed data for n subjects and encompasses all information about (longitudinal data, survival data, and covariates). The choice of prior distributions is crucial in Bayesian analysis. Priors should be chosen to reflect reasonable ranges for the parameters and can be either informative (based on previous studies or expert opinion) or weakly informative (to regularize the estimation without strongly influencing the results). And in this study all the standard prior distribution for all parameters [35] from the JMbayes package is considered. We assign appropriate prior distributions to all parameters. For example:\(\beta \sim N\left({\mu }_{\beta ,}{\Sigma }_{\beta }\right)\); A Normal prior for fixed effects in the longitudinal submodel. The mean \({\mu }_{\beta ,}\) represents our prior expectation for the effects, and the covariance matrix,\({\Sigma }_{\beta }\), reflects the uncertainty in that expectation. \(\alpha \sim N({\mu }_{\alpha },{{\sigma }_{\alpha }}^{2})\); A Normal prior for the association parameter. If we believe the longitudinal process increases the hazard, we might choose a positive \({\mu }_{\alpha }\),\(\gamma \sim N\left({\mu }_{\gamma ,}{\Sigma }_{\gamma }\right)\); A Normal prior for fixed effects in the survival sub-model and\({D}^{-1}\sim Wishart(v,V)\); A Wishart prior for the inverse of the random effects covariance matrix. Before begin estimation the missing data is imputed using Multivariate Imputation by Chained Equations or mice() function [36]. Because the posterior distribution is typically intractable, we use Markov chain Monte Carlo (MCMC) methods, such as Gibbs sampling or Metropolis–Hastings algorithms to draw samples from it. These samples allow us to approximate the posterior distribution and calculate quantities of interest, such as; Posterior means: Estimates of the model parameters, Posterior standard deviations; Measures of uncertainty in the parameter estimates, Credible intervals: Ranges of values that are likely to contain the true parameter value with a certain probability.

Model selection is a crucial step in statistical modeling, and two of the most commonly used criteria for this purpose are Akaike’s Information Criterion (AIC) and Bayesian Information Criterion (BIC). These criteria provide a trade-off between model fit and complexity. They are defined as follows:

where npara represents the number of parameters in the model, and n is the sample size. The preferred model is the one with the lowest value of the corresponding criterion, as it indicates a better balance between goodness-of-fit and complexity.

To compare different longitudinal models and joint models, we also analyzed the Bayesian deviance term, which is generally expressed as:

Furthermore, we assessed model fit using the Deviance Information Criterion (DIC). This criterion evaluates model adequacy while penalizing excessive complexity, ensuring a trade-off between goodness-of-fit and over fitting risk. The DIC is defined as:

where: \(E[D\left(\theta ,{b}_{i}\right)]\) is the posterior mean deviance (average deviance over the posterior distribution). \(D\left(\overline{\theta },{\overline{b} }_{i}\right)\); is the deviance evaluated at the posterior mean of the parameters. \({P}_{D}\) represents the effective number of parameters, acting as a penalty term to adjust for model complexity. A lower DIC value indicates a model with better fit and lower complexity, making it preferable for selection. A higher \({P}_{D}\) indicates a more complex model, potentially leading to over fitting, while a lower \({P}_{D}\) suggests a simpler model with fewer effective parameters [37].

The data for this study consists of 257 patients who are bipolar disordered individuals under psychiatric follow-up from first September 2018 to first January 2020 in JUMC. Since this dataset is longitudinal, even though the sample size is 257, there are missing observations. To ensure the accuracy of the descriptive analysis, I removed missing observations. By removing them, the dataset becomes more complete, making comparisons between recovered and non-recovered patients more meaningful. Among the total bipolar disordered individuals during the period, 116(45.1%) of them faced symptomatic recovery, whereas 141(54.9%) were censored. As observed from Table 1 below, 100(38.9%) are females, and 63(24.5%) of them have not recovered, whereas 37(14.4%) of them show symptomatic recovery, and 157(61.1%) are males, and 77(30.4%) of them have not recovered, whereas 79(30.7%) of them showed symptomatic recovery.

The majority of bipolar disorder patients 128(49.7%) are found in the 26–49 age category, and 67(26%) of them have not recovered, whereas 61(23.7%) of them show symptomatic recovery. Many of the bipolar disorder patients 145(56.6%) are single in marital status, and 90(35.2%) of them were not recovered, whereas 55(21.5%) of them show symptomatic recovery compared to other marital categories. Based on the relapse status of bipolar disorder patients, those who have not faced an event of relapse before the study are 66(25.7%) and are more likely to face an event of recovery relative to those who had faced an event of relapse before the study 50(19.5%).Many bipolar disorder patients have faced their first bipolar disorder episode at their adolescence age 119(46.5%) relative to other age categories, and 62(24.2%) of them have not recovered, whereas 57(22.3%) of them have recovered. Many bipolar disorder patients with the manic type of episodes are 153(60.5%), and 80(31.6%) of them have not recovered, whereas 73(28.9%) of them have recovered relative to other types of episodes. Considering family history of mental illness, 163(65.2%) of patients do not have a family history of mental illness, of which 82(32.8%) have not recovered, whereas 81(32.4%) have recovered. Meanwhile, 87(34.8%) have a family history of mental illness, with 52(20.8%) not recovered and 35(14%) recovered. With respect to substance abuse, 160(63%) of the patients do not use substances, with 83(32.7%) not recovered and 77(30.3%) recovered. On the other hand, 94(37%) are substance users, with 59(23.2%) not recovered and 35(13.8%) recovered. With regard to religion, 148(57.5%) of the bipolar disorder patients are Muslim, of which 99(38.5%) have not recovered, whereas 49(19%) have recovered. Orthodox Christians account for 64(25.5%), with 22(8.5%) not recovered and 44(17%) recovered. Protestant Christians are 35(13.6%), with 17(6.6%) not recovered and 18(7%) recovered, while 9(3.4%) belong to other religions, with 2(0.7%) not recovered and 7(2.7%) recovered.

In terms of khat chewing, 140(55.6%) of patients do not chew khat, and 73(29%) of them have not recovered, whereas 67(26.6%) of them have recovered. However, 112(44.4%) of the patients chew khat, with 68(27%) not recovered and 44(17.4%) recovered. Regarding educational status, 125(55.8%) of patients are tenth grade and below, with 75(33.5%) not recovered and 50(22.3%) recovered. Those with education above tenth and diploma are 64(28.6%), of which 30(13.4%) have not recovered and 34(15.2%) have recovered, while those with degree and above are 35(15.6%), with 21(9.4%) not recovered and 14(6.2%) recovered. In terms of bipolar type, 204(79.4%) of patients are type I patients, and 108(42%) of them have not recovered, whereas 96(37.4%) of them have recovered. However, 53(20.6%) of the patients are faced Type II, with 33(12.8%) not recovered and 20(7.8%) recovered. Among the total bipolar disorder patients, the high number of patients, 223(86.8%), are Oromo by ethnicity, and 127(49.4%) of them have not recovered, whereas 96(37.4%) of them have recovered. 18(7%) of them are Amhara, of which 7(2.7%) have not recovered, whereas 11(4.3%) have recovered. The other ethnicities are 16(6.2%), of which 6(2.3%) of them have not recovered, whereas 10(3.9%) of them have recovered. Regarding employment status, 190(77.7%) of the bipolar disorder patients are unemployed, of which 117(47.7%) have not recovered, whereas 73(30%) have recovered. Employed patients are 55(22.3%), with 23(9.3%) not recovered and 32(13%) recovered. Finally, concerning other cofactors, 131(51%) of patients have no other cofactors, with 55(21.4%) not recovered and 76(29.6%) recovered. On the other hand, 126(49%) have other cofactors, of which 86(33.5%) have not recovered, whereas 40(15.5%) have recovered.

Exploratory analysis of longitudinal data aims to discover patterns of systematic variation across groups of patients and characteristics of random variation that characterize separate patients. Figure 1 on the left-hand side below indicates the individual profile plot of 16 randomly selected individuals with the burden of bipolar symptoms. It indicates within and between subjects variability on the burden of bipolar symptoms over time. Close inspection of the shapes of the burden of bipolar symptom profiles indicates that for some individuals, these seem to be nonlinear. Therefore, during fitting later in JMbayes, regression splines are required to estimate the baseline relative risks. On the right-hand side, the overall individual curves with the loess smoothing technique suggest the linear growth effect in the mean structure of burden of bipolar symptoms over time. Therefore, the linear time effects should include fixed and random effects in the model and indicate that the mean burden of bipolar symptoms decreases over time. We are exploring the Mean Structure to understand the possible relationships among the burden of bipolar symptoms, a plot of a line connecting the average values computed at each time point like the Fig. 2 below. Then mean structure plot suggests that the mean burden of bipolar symptoms profiles has a nonlinear growth over time.

Individual profile plot of 16 random sampled individuals and overall individual profile plot with loess curve over time

Full size image

Mean of burden of bipolar symptoms over time

Full size image

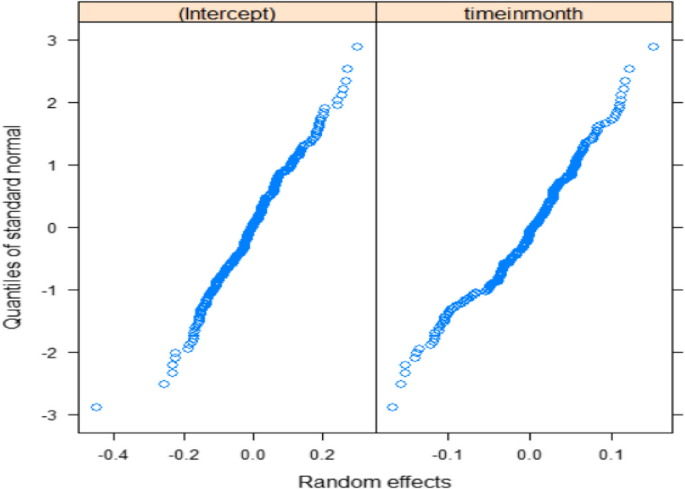
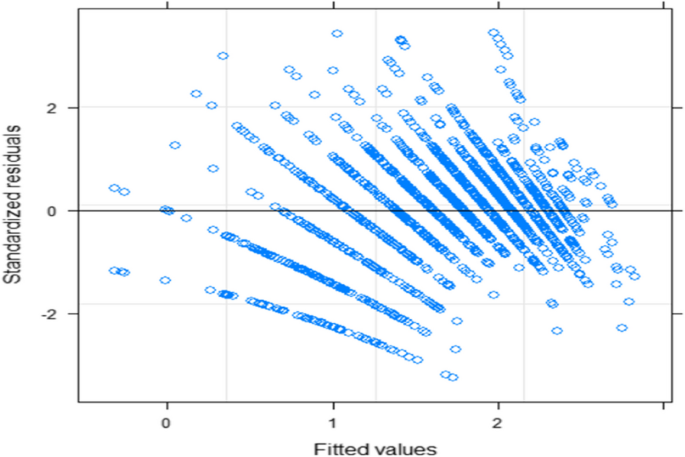
The generalized linear mixed model is built within two stages; the first stage involves fitting generalized linear regression models, which only considers the subjects'variability and an appropriate fixed effect for the outcome variable based on the AIC values of the fitted candidate GLM. The fitted model explains the burden of bipolar symptoms by accounting only for the variability of the bipolar disordered patients. The dispersion parameter for poison distribution is taken to be one, and the residual deviance is equal to the degrees of freedom so that no over-dispersion indicates there is no over-dispersion. The variance of the poison distribution is taken to be equal to its mean. Then, the poison distribution is appropriate for this study to fit both GLM and GLMM. As reported in Table 2 below, seven generalized linear mixed models are fitted with different time random effects from random intercept to random intercept; linear and quadratic time slopes use Laplace approximation. Among the seven fitted GLMM, random linear slope time effect is selected as best time random effect with small 8494.9 AIC and 8663.5 BIC values and based significance value of chi-square test. The final appropriate GLMM for the separate longitudinal model is fitted using both Laplace and then Penalized quasi-likelihood approximation as reported in Table 3. The independence and normality assumption diagnosis of the random effects was checked using residual versus fitted value, and quantile quantile plots shown in Figs. 3 and 4 and the plots show no problems of the normality assumptions.

Q-Q Plot for Assessing Normality of Random Effects in Generalized Linear Mixed Effects Model

Full size image

Plot of standardized residuals against fitted values in generalized linear mixed effects model

Full size image

Kaplan–Meier survival function estimates

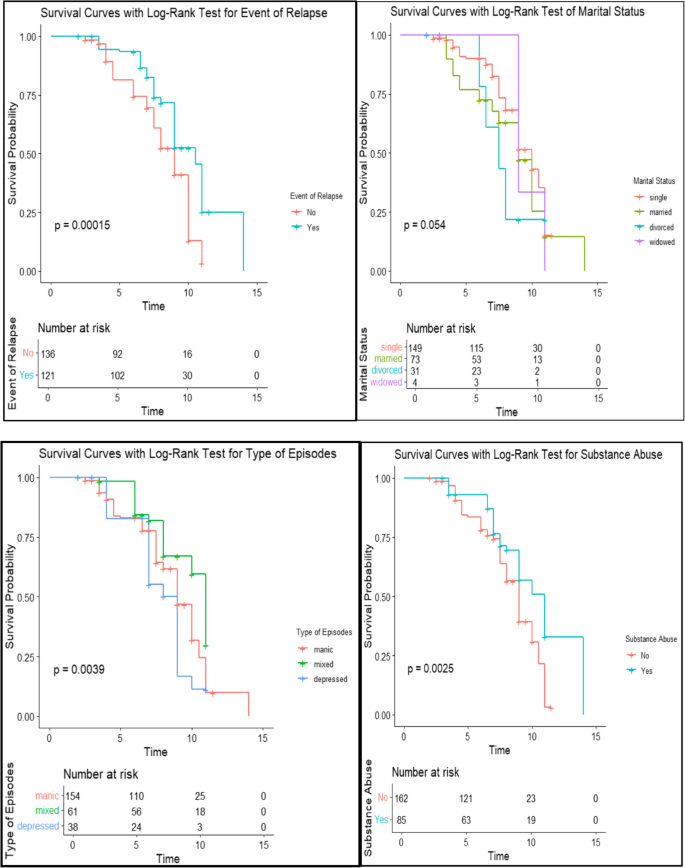
The Kaplan Meier estimate is the most common-parametric technique for modeling the survival function. It was applied to estimate the survival curves for categorical covariates and the estimated survival probability curve of some selected categorical covariates. The Kaplan-Meir estimated median value that the half of the bipolar disorders experiencing the event was nine months. From the Fig. 5, we can see that those single individuals have the highest probability curve of time to recovery. The divorced individual has the lowest probability curve of time to recovery relative to the marital status of other groups. Substance abuse patients have a higher time to recovery relative to those who do not use substance abuse. The patients who have faced the event of relapse have a higher time to recovery relative to those who do not face the event of relapse. The patients with mixed types of bipolar episodes have a higher time to recovery relative to those with manic and depressive episodes. However, patients with manic episodes have a higher time to recovery relative to those with depressive episodes.

Kaplan–Meier survival curves with log-rank test for event of relapse, marital status, episode types, and substance abuse in bipolar patients

Full size image

From Fig. 5, we can see that those single individuals have the highest probability curve of time to recovery. The divorced individual has the lowest probability curve of time to recovery relative to the marital status of other groups. The patients who face an event of relapse have a high probability curve of time to recovery relative to those who do not face an event of relapse. Substance abuse patients have a higher time to recover than those who do not use substance abuse. The patients who had faced an event of relapse before had a higher time to recovery relative to those who had not faced any event relapse.

Result of cox-proportional hazard model

From Table 4, we are using AIC for variable and model selection in our study. Then the variables marital status, religion, age, the event of relapse, bipolar type, types of episodes, and substance abuse significantly affect the time to symptomatic recovery of bipolar disorder. The results of a Log-Rank test, which is a statistical test used to evaluates whether the survival curves (time-to-symptomatic recovery) differ significantly across levels of categorical variables. A statistically significant result (p < 0.05) indicates that the time-to-symptomatic recovery varies across the groups defined by the categorical variable. For variables with a p-value less than 0.05 (Religion, Age, Event of relapse, Type of episodes and Substance abuse), there is a statistically significant difference in the time-to-symptomatic recovery curves between the different categories of that variable. This means that patients in different categories of these variables have different recovery trajectories. For Bipolar type variables with a (p ≥ 0.05) there is no statistically significant difference in the time-to-symptomatic recovery curves between the different categories of that variable. This means that patients in different categories of these variables have similar recovery trajectories. Overall, these findings could guide clinicians in tailoring interventions by focusing on modifiable factors like event of relapse management or addressing substance abuse.

From Fig. 6, the lines appear to be somewhat parallel, especially in the earlier time points. However, there seems to be a slight divergence in the later time points. This suggests that the proportional hazards assumption might be violated to some extent.

Log-Minus-Log survival curves for assessing proportional hazards assumption

Full size image

From Table 5 a statistically significant p-value (p < 0.05) indicates a violation of the proportional hazards (PH) assumption, suggesting that the covariate’s effect on survival is time-dependent. The global test (χ2 = 52.80, df = 14, p = 0.00) is significant, indicating that the model overall does not satisfy the PH assumption. This suggests that multiple covariates have time-varying effects on the hazard, necessitating adjustments such as incorporating time-dependent covariates or alternative modeling strategies to ensure accurate predictions. Bayesian joint models address violations of the Cox proportional hazards (PH) assumption by incorporating flexible modeling strategies that adapt to time-varying relationships between covariates and the hazard function. Bayesian joint models integrate longitudinal processes (repeated measurements) as dynamic predictors of the survival outcome. These predictors naturally account for time-dependent effects since they evolve with time, enabling the hazard function to change in response to the trajectory of the longitudinal variable. Additionally, random effects in the longitudinal component of the joint model can further capture individual-specific variations in the hazard. To explicitly relax the PH assumption, Bayesian joint models allow for time-dependent covariates, either by directly including interaction terms between covariates and time or by using splines or other flexible priors to model time-varying effects. This makes Bayesian joint models particularly suited for real-world data, where strict proportionality often does not hold, and the relationship between covariates and survival outcomes is more dynamic [30].

Based on the GLMM that incorporates subject-specific variance under longitudinal sub-model and semi-parametric model under survival sub-model, we explore several joint models with various latent processes. The”param” specifies the association structure between the longitudinal and survival processes in this study. The”shared-RE” association structure is used in which only the random effects of the generalized linear mixed model are incorporated in the linear predictor of the survival sub-model. Moreover, the GLMM is obtained using argument densLong since the response variable for this study is count and follows the Poisson distribution. The glmmPQL() function from a MASS package generates GLMM using penalized quasi-likelihood. In this study, the Bayesian method results are based on four parallel MCMC sampling chains of 20,000 iterations each, following a 3000 discarded as burn-in to achieve convergence. Several joint models using different shared parameter association structures with different combinations of the random effect processes are fitted. Then in this study, a shared parameter association structure is selected based on the smallest DIC value of the joint models, reported in Table 6.

Because Model II emerges with the smallest total DIC 9207.546 among all other models, it is selected as the final joint model for the burden of bipolar symptoms and time to symptomatic recovery of bipolar disorder. We have used a time series plot of the history of iterations of the final Bayesian joint model, which shows a reasonable degree of randomness between iterations Fig. 7 is used to check the MCMC chains'convergence. The overlaps of the three chains indicate that the exact solutions are obtained for each initial value. Therefore, the Gibbs sampler has converged to the target density.

Trace plot of time series iteration of Gibbs sampling to check convergence

Full size image

As observed from Table 7, the appropriate joint model with a minimum DIC (Deviance Information Criteria) score values than the remaining joint models is selected. The longitudinal sub-model specification is the same as the selected generalized linear mixed model. In contrast, the survival sub-model specification incorporates the association parameters to the selected cox-regression model. The posterior estimates of the longitudinal sub-model and survival sub-model regression coefficients with their 95% credible interval are summarized in Table 7. In the longitudinal sub-model, the variables; The intercept, time interval of follow up, 50 and above age group, the interaction between time interval of follow up and adolescent age first onset of the bipolar disorder, the interaction between time interval of follow up and event of relapse, the interaction between linear time interval of follow up and existence of other cofactors and the interaction of substance abuse and chewing khat are significantly affecting the log expected burden bipolar symptoms. Whereas in the survival sub-model, the covariates; divorced, marital status, event of relapse, mixed type of episodes significantly affect the symptomatic recovery of bipolar symptoms. α₀ = − 8.403 explains the association between longitudinal and time-to-event outcomes with [- 11.157,− 6.576] credible interval. It associates longitudinal count, the burden of bipolar symptoms, and time-to-symptomatic recovery of bipolar disorder using shared random effect parameters. We observe a significantly strong negative association between the subject-specific random intercept (baseline) of the burden of bipolar symptoms and the risk ratio of symptomatic recovery since their 95% credible intervals exclude zero. The σb0 = 0.410 indicates the heterogeneity in the longitudinal measurement of the burden of bipolar symptoms that must be accounted for. The mean burden of bipolar symptom scores at baseline for a reference individual is estimated at 0.410. This study's Bayesian results are based on four parallel MCMC sampling chains with 20,000 iterations each following a 3000 discarded burn-in to achieve convergence.

Table 8 shows the Coefficient and hazard ratios of the standard relative risk model to determine the hazard of symptomatic recovery using baseline covariates and with the assumption of a time-independent covariate. The risk ratio value of 1 means no difference in relative risk between groups. When the relative risk is less than one, the corresponding covariate has negatively affected the event of interest. When it is greater than one, the corresponding covariate positively affects the event of interest. From Table 8, we observed that; the risk of symptomatic recovery time for divorced bipolar disorders is greater than the single bipolar disorder given the burden of burden bipolar of symptoms. The risk of time to symptomatic recovery for between twenty and twenty-five is 7.110 greater than those nineteen and below nineteen age groups, given the burden of bipolar symptoms.

The risk ratio of recovery time for the fifty and above the age group of bipolar disorders is less than those nineteen and below age groups given burden bipolar symptoms. The risk of recovery time for bipolar disorders those faced events of relapse before is less than for those who did not face an event of relapse before, given the burden of bipolar symptoms.

The relative risk of recovery time for bipolar disorders with bipolar II is 30.2% less than those with bipolar I, given the burden of bipolar symptoms. The relative risk of recovery for bipolar disorders with mixed episodes is less than those with manic episodes, given the burden of bipolar symptoms. The hazard of recovery for bipolar disorders with depressed episodes is more significant than those with manic episodes, given the burden of bipolar symptoms. The risk of recovery for substance abuse bipolar disorders is less than those not abused substances, given the burden of bipolar symptoms. The relative risk of symptomatic recovery time for bipolar disorders at baseline time (random intercept) indicates that the one unit increase in the burden of bipolar symptoms at a starting point in time results in a 0.001(0.1%) decreased risk of time to symptomatic recovery with a 95% credible interval of [0.000, 0.002]. These results are statistically significant since its credible interval excludes zero, indicating that the burden of bipolar symptoms is a good predictor of time to symptomatic recovery.

This study explores the benefits and applications of Bayesian joint models in analyzing longitudinal and survival data within the context of bipolar disorder research. In particular, we highlight the advantages of this approach when the primary objective is to understand the influence of longitudinal symptom burden on time to symptomatic recovery. By simultaneously modeling these processes, joint models yield less biased and more efficient estimates of the effect of longitudinal symptom trajectories on time to event, especially when compared to analyzing the data separately. A key advantage is the ability to account for the complex interplay between repeated measurements of individual bipolar symptoms over time and the eventual time to recovery. Therefore, this work demonstrates the potential of joint modeling as a powerful alternative to traditional methods when predicting individual symptomatic outcomes in bipolar disorder, offering a more comprehensive and nuanced understanding of disease progression and recovery.

A Bayesian joint model was proposed to simultaneously analyze longitudinal count data representing the burden of bipolar symptoms and time-to-event data representing symptomatic recovery. The longitudinal process, capturing the evolution of symptom burden, was modeled using a Poisson mixed-effects model. This model allows for subject-specific random effects b_i to account for heterogeneity in baseline symptom levels and rates of change. The time-to-recovery process is modeled using a Cox proportional hazards model. The joint model connects these two processes by incorporating the random effects b_i from the longitudinal Poisson model into the hazard function of the Cox model. This shared parameter approach assumes that individual trajectories of symptom burden, as characterized by the random effects, are predictive of the time to symptomatic recovery. The Bayesian framework allows for the incorporation of prior information and provides a natural means for quantifying uncertainty in parameter estimates within both the longitudinal and survival components.

In this study, among the 257 bipolar disorders under psychiatric follow-up during the period, 116(45.1%) of them faced symptomatic recovery, and 141(54.9%) were censored. Similarly, the department of psychiatry at the University of Cincinnati, College of Medicine shows symptomatic recovery occurred in only 26% of disorders among 134 total bipolar disorders [35]. Another study shows that of 1,469 participants symptomatic at study entry, 858 (58.4%) subsequently achieved recovery, which also supports this study. The study done on the Longitudinal Course of Bipolar-I Disorder and Duration of Mood Episodes [20] to describe the duration of bipolar I mood episodes and factors associated with recovery from these episodes while the probability of recovery over time from multiple successive mood episodes is examined with analytical survival techniques, which showed that the median duration of bipolar I mood episodes was 13 weeks which support the result of this study [36]. This study reveals that the interaction between time in a month and adolescent age first onset of the bipolar disorder significantly affects the log expected burden of bipolar symptoms. And it is supported by the idea that people with bipolar disorder have highly disruptive episodes, frequent recurrences, and severe psychosocial impairments, and the illness typically has its onset in adolescence and even late childhood in some patients [38].

This study shows that the hazard of recovery for bipolar disorders with the depressed type of episodes is more significant than those with the manic type of episodes given the burden of bipolar symptoms with a 95% credible interval of [1.737, 7.500], which agrees with the study by Solomon [20] showed that the probability of recovery from a major depressive episode was a significantly more prominent chance of recovery from an episode of mania (HR = 1.713; 95% and Confidence interval of [1.373, 2.137]. This study shows that the relative risk of recovery for bipolar disorders with mixed types of episodes is less than those with manic episodes given the burden of bipolar symptoms, which disagrees with the study done using multivariate analyses [35] suggests that; during the 12-month follow-up period, there were no significant differences in outcome between patients with manic compared with mixed Bipolar disorder. And this may be due to the inefficient model he uses, which means using the Joint model may improve the efficiency and biasedness of the estimator. Bayesian methods of joint modeling enabled the specification of a time-varying coefficient to link the longitudinal and the survival processes. Which, Andrinopoulou looked at the valve function of cardiac-thoracic surgery, which is monitored over some time [30].

To examine the association between longitudinal symptom burden and time to symptomatic recovery in bipolar disorder, this study implements a Bayesian joint model with a shared parameter structure [39]. This structure links the longitudinal and survival sub-models, allowing symptom trajectories to predict the hazard of recovery. The baseline hazard function in the survival process is estimated using regression splines within the Bayesian framework [30]. In this study the joint models are estimated under the Bayesian framework using a four chain of 20,000 MCMC iterations from which we discarded the first 3,000 samples as burn-in; finally, trace time series plots are plotted for the convergence diagnosis of MCMC samples, and in the plots, there is not any problem of convergence failure. Our results support the hypothesis of an association between time to symptomatic recovery and the burden of bipolar symptoms. We found that the hazard of symptomatic recovery increases by decreasing the burden of bipolar symptoms, indicating a negative relationship. And, we hypothesize that individuals with a higher initial symptom burden or a slower rate of symptom reduction (captured by b_i) will experience a longer time to recovery.

BD:

Bipolar Disorder

CI:

Confidence Interval

Cis:

Credible intervals

GLM:

Generalized Linear Model

GLMM:

Generalized Linear Mixed Model

MCMC:

Markov chain Monte Carlo

DIC:

Deviance Information Criteria

P_D :

Effective Number of Parameters

PH:

Proportional Hazards

PMF:

Probability Mass Function

Download references

The corresponding author, Tefera Fufa (M.Sc. in Biostatistics), made an outstanding commitment regarding the conception, work detail, design, analysis, interpretation, and compilation of the study. The other authors took part in drafting, reexamining, and checking on the article, provided the last approval of the version to be allocated, agreed on the journal to which the article has been submitted, and were responsible for all aspects of the work

Correspondence to Tefera Fufa Kulute.

Ethical approval was waived by the local Ethics Committee of the College of Natural Sciences, Jimma University, Ethiopia. In the view of the retrospective nature of the data and all the procedures being performed were parts of the routine care.

This study utilized secondary data from existing patient records. As such, direct informed consent from individual patients was not obtained. However, all patient data was handled in accordance with relevant ethical guidelines and privacy regulations. The study protocol was reviewed and approved by the Jimma University Review Board or Ethics Committee. The authors have taken all necessary steps to ensure patient confidentiality and anonymity through the research process.

All the methods were performed in accordance with relevant guidelines and regulations.

Not applicable.

The authors declare no competing interests.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions