BMC Medical Informatics and Decision Making volume 25, Article number: 162 (2025) Cite this article
Malaria, an infectious disease caused by protozoan parasites belonging to the Plasmodium genus, remains a significant public health challenge, with African regions bearing the heaviest burden. Machine learning techniques have shown great promise in improving the diagnosis of infectious diseases, such as malaria.
This study aims to integrate ensemble machine learning models and Explainable Artificial Intelligence (XAI) frameworks to enhance the diagnosis accuracy of malaria.
The study utilized a dataset from the Federal Polytechnic Ilaro Medical Centre, Ilaro, Ogun State, Nigeria, which includes information from 337 patients aged between 3 and 77 years (180 females and 157 males) over a 4-week period. Ensemble methods, namely Random Forest, AdaBoost, Gradient Boost, XGBoost, and CatBoost, were employed after addressing class imbalance through oversampling techniques. Explainable AI techniques, such as LIME, Shapley Additive Explanations (SHAP) and Permutation Feature Importance, were utilized to enhance transparency and interpretability.
Among the ensemble models, Random Forest demonstrated the highest performance with an ROC AUC score of 0.869, followed closely by CatBoost at 0.787. XGBoost, Gradient Boost, and AdaBoost achieved ROC AUC scores of 0.770, 0.747, and 0.633, respectively. These methods evaluated the influence of different characteristics on the probability of malaria diagnosis, revealing critical features that contribute to prediction outcomes.
By integrating ensemble machine learning models with explainable AI frameworks, the study promoted transparency in decision-making processes, thereby empowering healthcare providers with actionable insights for improved treatment strategies and enhanced patient outcomes, particularly in malaria management.
The development of machine learning has brought about the era of predictive analysis in medical systems, promising more effective patient care and efficient medical practices. With the growing volume and complexity of healthcare data [1], there is an increasing need for accurate prediction models. However, in addition to accuracy, these models must be transparent and interpretable, especially about sensitive health information that directly affects patients’ health [2,3,4]. Health providers are challenged by making decisions based on huge amounts of available information while keeping their predictions reliable and trustworthy [5]. Traditional machine learning algorithms are often called black boxes because they often cannot explain why they have chosen this or that action [6, 7].
The ensemble models proposed in this study aim to achieve improved accuracy while maintaining transparency and interpretability [8]. Ensemble methods, such as bagging, boosting, and stacking, harness the strengths of multiple models to enhance predictive performance [9]. For instance, bagging reduces variance by averaging predictions from various models trained on different data subsets, while boosting focuses on sequentially training models on the errors of prior models to improve accuracy. Stacking combines predictions from multiple models using a meta-model, allowing for the capture of more complex data relationships. However, this study emphasizes simpler ensemble methods that effectively balance accuracy with transparency, avoiding the increased complexity associated with stacked algorithms, which may hinder interpretability. Ensemble learning has shown great promise across various fields, including healthcare, agriculture, and sports science. In healthcare, methods such as random forests and boosting techniques have improved predictive accuracy for conditions like diabetes and heart disease [10]. In agriculture, ensemble methods have been utilized for predicting crop yields and identifying pest infestations, showcasing their versatility in diverse domains [11]. Similarly, in sports science, ensemble techniques have been employed for performance prediction and injury risk assessment, providing coaches and athletes with actionable insights [12]. These applications underscore the potential of ensemble methods to enhance predictive modeling in healthcare, particularly for complex diseases such as malaria.
Malaria continues to pose a significant public health challenge globally, particularly in regions where the disease is endemic. In 2022, the World Health Organization (WHO) reported 249 million malaria cases and 608000 mortality globally due to malaria [13]. The African region was also reported to bear the heaviest burden of malaria with 95% of incidence and 94% mortality resulting from malaria in this region [13]. Furthermore, Nigeria has been reported as one of the five countries with the highest reported cases of malaria (WHO, 2023). In Nigeria, 80% of deaths resulting from malaria occur among children who are below the age of five [14]. Frequent malaria re-infections during childhood places a huge economic burden on the entire healthcare system. The situation is further worsened by the development of resistance to commonly used antimalarial medications [15]. Malaria is caused by the protozoan parasite-Plasmodium, of the phylum Apicomplexa. It thrives in warm tropical climates, predominantly transmitted by the female Anopheles gambiae mosquito. The Plasmodium species, carried by a vector, infects a wide range of vertebrates ranging from mammals, birds, amphibians, and humans. It consists of six species that cause infection in humans. These are Plasmodium falciparum, Plasmodium malariae, Plasmodium ovale, Plasmodium vivax, and the zoonotic Plasmodium knowlesi and Plasmodium cynomolgi. Plasmodium falciparum is the most deadly and prevalent among these species [15]. The transmission of the malaria parasite is closely tied to environmental conditions that allows mosquito to thrive, especially high and humid temperatures after rain. Hence, the reason why Africa bears the heaviest burden of Malaria [16].
Clinical signs and symptoms of malaria typically manifest during the intra-erythrocytic stage of the disease. At this stage, mature schizonts release merozoites that cause the rupture of red blood cells (RBCs), triggering the onset of fever-a hallmark symptom of malaria. This process can also lead to severe complications such as malaria-induced anemia, particularly in children, due to significant RBC destruction. Additional symptoms include chills, headaches, and vomiting, which are common to other febrile illnesses as well [17]. Consequently, the use of precise diagnostic tools is crucial to detect and manage malaria. In regions where malaria is endemic, many individuals harbor the infection without showing symptoms, thanks to acquired immunity. These asymptomatic infections often go undetected by standard field diagnostics such as optical microscopy (detection limit: 50 parasites/\(\upmu\)L) and rapid diagnostic tests (detection limit: 100–200 parasites/\(\upmu\)L), particularly when parasite levels are low [18]. Nonetheless, these undetected infections contribute to the persistence of malaria, as mosquitoes that bite infected carriers can acquire and then transmit the parasite to others, perpetuating the spread of the disease. Without appropriate treatment, these infections can lead to severe health consequences. Moreover, asymptomatic carriers pose a risk of spreading malaria through mechanisms such as imported cases, or via blood transfusions and organ transplants [18].
There is a critical need for more effective diagnostic tools that can identify such low-density infections to prevent the spread of malaria both within endemic regions and globally. Early treatment of these infections moves us closer to the goal of global malaria elimination. Additionally, the ability to promptly identify parasite strains is vital to curb the spread of drug resistance.
Machine learning has emerged as a reliable diagnostic tool in the detection of various diseases, including malaria. It offers the potential to detect infections early and accurately, ensuring the correct administration of antimalarial drugs and reducing the risks associated with drug overuse and misuse. Timely and accurate diagnosis is crucial for effective treatment and management, yet traditional diagnostic methods often face limitations in sensitivity and accessibility, especially in low and middle-income countries where access to medications, health care, and preventive education is limited [14]. In recent years, advancements in machine learning (ML) techniques have shown promise in enhancing the accuracy of infectious disease diagnosis through automated analysis of medical images and clinical data [19]. However, the complexity of modern ML models, such as deep learning networks [16], can hinder their adoption in clinical settings due to their inherent lack of interpretability. Healthcare professionals require transparent and explainable models to trust and effectively utilize these technologies. Explainable ensemble machine learning models offer a compelling solution by combining the high predictive power of ensemble learning with enhanced interpretability, thereby bridging the gap between accuracy and transparency in malaria diagnosis [16].
Machine learning techniques have proven valuable in healthcare diagnostics, as demonstrated in [20]. Their study uses advanced feature selection methods, including bio-inspired algorithms like Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Firefly Algorithm (FA), combined with ensemble models (RF and XGBoost) to enhance the accuracy of depression diagnosis. These methodologies parallel our approach in malaria diagnostics, where robust feature selection and ensemble models are utilized to maximize accuracy and interpretability. The study underscores the broader applicability of ML in healthcare, providing a framework for enhancing diagnostic efficiency.
Recent advancements in machine learning for medical diagnostics are exemplified by [21], who conducted a systematic review of ML techniques in depression diagnosis. The study highlights the effective fusion of ML techniques with diverse data modalities, emphasizing the importance of careful pre-processing and feature optimization. These findings resonate with our study’s approach to malaria diagnostics, where ensemble models are employed to enhance accuracy and robustness. The review further underscores shared challenges, such as data scarcity, that motivate the adoption of advanced handling techniques. [22] highlights the application of machine learning models, such as Random Forest (RF) and Gradient Boosting (GB), to predict malaria using patient clinical information rather than blood smear images. Key contributions include the use of SMOTE to address class imbalance and the identification of critical features like nationality (for imbalanced data) and symptoms (for SMOTE-balanced data) in malaria prediction. These findings resonate with our use of SMOTE and feature importance analysis in our ensemble models, such as Random Forest and CatBoost, for malaria diagnosis.
[23] Barboza et al. focus on spatiotemporal prediction of malaria cases in the state of Amazonas, Brazil, using a large dataset of approximately 6 million records. By clustering cities based on malaria incidence and employing machine learning (ML) and deep learning (DL) models such as Random Forest, Long Short-Term Memory (LSTM), and Gated Recurrent Units (GRU), the study demonstrates the effectiveness of ML/DL models in predicting malaria cases. The results highlight that GRU performs better in regions with high variability in malaria incidence, while LSTM excels in regions with low variability. Our study differs by focusing on patient-level data and employing ensemble methods like Random Forest and CatBoost for malaria diagnosis. While Barboza et al. address macro-level prediction for resource allocation, our approach aims to improve clinical diagnostics through explainable AI (XAI). Together, these studies emphasize the versatility of ML/DL models in tackling malaria from both public health and clinical perspectives.
The study by [24] explores the application of Variational Quantum Circuit (VQC) machine learning for malaria diagnosis, leveraging the hybrid capabilities of quantum-classical computing. This innovative approach utilizes red blood cell (RBC) images and employs advanced feature optimization techniques, including Minimum Redundancy Maximum Relevance (mRMR) and Principal Component Analysis (PCA), to refine the feature set. By optimizing both the input encoding and the parameters of the quantum circuit, the VQC model demonstrates the potential of quantum-enhanced learning to achieve superior performance with reduced computational complexity. The study reports impressive metrics-99.06% accuracy, 99.08% precision, 99.05% recall, and 99.07% specificity-using 10-fold cross-validation. Additionally, the authors incorporate a rule-based expert system to classify malaria types, further enhancing the model’s clinical utility. The research not only highlights the growing role of quantum machine learning in healthcare but also establishes a benchmark for future studies exploring quantum approaches in diagnostic systems. Compared to our study, which utilizes ensemble machine learning on clinical data, the VQC approach focuses on image-based data and quantum computing. While both emphasize feature optimization for accuracy, our work prioritizes explainability through SHAP and LIME, advancing interpretability and clinical relevance, whereas VQC highlights computational efficiency.
Our study explores the application of explainable ensemble machine learning models in malaria diagnosis, aiming to improve diagnostic accuracy while providing insights into the decision-making process of these models. By examining these models’ methodologies, benefits, and challenges, we seek to highlight their potential to revolutionize malaria diagnostics and contribute to better healthcare outcomes worldwide. Additionally, the findings from this study will be helpful for healthcare practitioners, policymakers, and researchers to select the most suitable models for health data prediction, thereby advancing the integration of machine learning in healthcare and fostering a more efficient and effective healthcare system. This study employs three primary methodologies in conjunction with ensemble techniques: Local Interpretable Model-agnostic Explanations (LIME) [25], Shapley Additive Explanations (SHAP) [26], and Permutation Feature Importance (PFI) [27]. LIME assists in explaining the predictions of black-box models by creating surrogate models with interpretable local behavior. SHAP, on the other hand, provides a unified measure of feature importance by assigning each feature an importance value for a particular prediction based on cooperative game theory principles. These methods enhance the interpretability of the models by illustrating how each feature contributes to the final prediction. PFI assesses the significance of each feature by determining how much the model’s performance decreases when its values are randomly permuted. By utilizing these methods, the ensemble models will become more comprehensible and dependable for healthcare professionals, enabling them to make informed decisions based on model predictions.
The research questions guiding this study are as follows:
In this study, we utilized a cross-validation strategy to ensure the robustness of our models. A 10-fold cross-validation was applied, which involves splitting the dataset into five subsets. For each fold, one subset is used as the validation set, while the remaining four subsets are used to train the model. This process is repeated five times, with each subset used as the validation set once. This helps to reduce overfitting and provides a more reliable estimation of model performance. We systematically optimized key hyperparameters for each model using RandomizedSearchCV with 5-fold cross-validation across multiple candidates. For Random Forest, we tuned the number of trees and maximum depth over 50 fits for 20 candidates. Similarly, boosting models such as AdaBoost, Gradient Boosting, XGBoost, and CatBoost were fine-tuned for parameters like learning rate, number of boosting iterations, and regularization terms, with 45–50 fits for 9–20 candidates each. These efforts significantly improved model performance, as detailed in the Model results section.
Ogun State is located in the Southeastern part of Nigeria. The State borders the Republic of Benin to the West, Osun and Oyo States to the north, Lagos State and Atlantic Ocean to the south and Ondo State to the east. Ogun State has a population density of 6,445,275 as of 2023 (National Population Commission, 2023). The State has a tropical wet and dry climate and has 224.18 rainy days yearly, hence a high breeding ground for Plasmodium.
The research pathway followed in this work can be seen from the illustration in Fig. 1. It gives a visual representation of the processes carried out in this work.
This section provides an overview of the data preprocessing methods utilized in this study.
Spearman Rank Correlation Coefficient
The Spearman Rank Correlation Coefficient, often denoted as \(\rho\) or \(r_s\), measures the strength and direction of a monotonic relationship between two continuous or ordinal variables. It ranges from −1 to 1, where:
Understanding the Spearman Correlation Coefficient is essential for analyzing relationships in our dataset, as it helps identify patterns and associations relevant to malaria-related data, even when relationships are not strictly linear.
The formula for Spearman’s correlation is based on the ranks of the data rather than the raw values:
$$\begin{aligned} r_s = 1 - \frac{6 \sum d_i^2}{n(n^2 - 1)} \end{aligned}$$
where: \(d_i\) is the difference between the ranks of each pair of values \((X_i, Y_i)\), n is the number of data points.
In this formula, each variable is ranked from smallest to largest, and the correlation is calculated on these ranks, making Spearman’s coefficient more robust for non-linear relationships .
Standardization
Standardization entails transforming the input data to have zero mean and unit variance. This is crucial in modeling since all inputs are scaled equally, thus avoiding the creation of biased models. Let a dataset contain n observations with p features, \(X_{j}, j=1,2, \ldots p\), then Eqs. (1) and (2) present the means and standard deviations of feature j correspondingly.
$$\begin{aligned} \varvec{\mu }_{\varvec{j}} = \frac{1}{n} \sum \limits _{i=1}^{n} x_{i} \end{aligned}$$
(1)
$$\begin{aligned} \varvec{\sigma }_{\varvec{j}} = \frac{1}{n} \sum \limits _{i=1}^{n} \left( x_{i} - \varvec{\mu }_{\varvec{j}}\right) ^{2} \end{aligned}$$
(2)
where \(\varvec{\mu }_{j}\) and \(\varvec{\sigma }_{j}\) are the mean and standard deviation of feature j respectively, \(x_{i}\) is the i-th observation in feature j, and n is the total observations. Standardization of an observation i for feature j using z-score normalization can be given by:
$$\begin{aligned} \textbf{X}_{\text {standardized}} = \frac{x_{i} - \mu _{j}}{\sigma _{j}} \end{aligned}$$
(3)
Standardization is an important technique in machine learning that helps improve the robustness and generalizability of models.
Over-sampling
Over-sampling is a technique used in machine learning to aid in addressing class imbalance. Chawla et al. [29] introduced it for the first time. The minority class will be enhanced by this way of replicating existing instances and making sure that each category has equal number of samples. This method functions very much like KNN. Considering X to be the input matrix having minority class instances, k being the number of nearest neighbors to be considered and m as the synthetic samples to generate. Let \(x_{i}\) represent an observation on a minority data point \(x_{ij}\) which is the ith observation on jth feature and k randomly selected neighbors. The new feature vector, \(X_{i, new}\), is defined as:
$$\begin{aligned} X_{j,\text {new}} = X_j + [\alpha (X_j - X_r)] \end{aligned}$$
(4)
Where \(X_j\) is the original feature vector, \(\alpha\) is any random number between 0 and 1, while \(X_r\) denotes a randomly chosen feature vector from all available vectors. Overfitting observed in random sampling can be mitigated through oversampling. Classification accuracy can improve if this technique is used [29].
Ensemble machine learning models are powerful techniques that combine multiple individual models to improve overall performance and robustness. The idea is that by integrating the predictions from several models, an ensemble can reduce the likelihood of errors and produce more accurate results compared to any single model. We describe the ensemble machine models used in this study in the following sub-sections:
Random Forest
Random Forest (RF) is a tree-based ensemble learning method, and bagging type ensemble [30]. Unlike other ordinary trees, RF splits every node by selecting the most effective among a random subset of predictors at that node [31]. This extra layer of randomness is what makes RF more resistant to over-fitting [32]. To improve the bagged trees in RF, a slight change that de-correlates the trees are made. For example, in bagging, we create several decision trees for bootstrapped training sets. However, when constructing these decision trees, each time a split occurs within a tree, a randomly chosen sample of m variables are selected as potential splitting points out of the complete set of p-predictors [33]. The random forest builds each decision tree as follows:
In deciding how to classify the data, each decision tree acts as an expert. The predominant result (majority vote) is used to make predictions after computing the prediction for each decision tree [34]. The optimal method for enhancing bagging is to reduce variation. This is such that the outcome for a B tree (bootstrap sample) is equal to the outcome for any other tree, and vice versa, due to the evenly distributed tree spread resulting from the bagging strategy. The B-bagged trees’ bias is, therefore, equal to the bias of an individual B tree.
The basic idea of RF is to enhance the bagging variance by reducing the correlation between trees [35]. This objective is accomplished during the tree-building process by randomly selecting input variables. Every node is divided from a subset of predictors chosen arbitrarily at every node into the best predictors. Prior to every split, RF chooses arbitrarily \(b \le a\) input variables as candidates for splitting where a is the overall number of input variables. Most of the time, b has a value of \(\sqrt{a}\) or possibly just 1 . Additionally, trees with particular framework qualities are produced by this choice at random. To obtain the final RF class prediction, we apply a majority vote on the RF’s respective decision trees. Specifically, let \(\hat{C}_{i}(y)\) denote the prediction made by the \(i^{t h}\) tree, then the RF prediction \(\hat{C}(y)\) is:
$$\begin{aligned} \hat{C}(y)=\text{ Majority } \text{ vote } \left\{ \widehat{C}_{i}(y)\right\} _{i=1}^{n}, \end{aligned}$$
(5)
where \(i=1, \cdots , n\) and n is the number of trees.
AdaBoost
Adaptive boosting (AdaBoost) algorithm is an ensemble learning technique that enhances the performance of weak learners to create a robust predictive model [36]. In Adaboost, training sets \((x_1 , y_1)\), \((x_2 , y_2 )\),. . . , \((x_m , y_m )\) is the input, where each \(x_i\) belongs to some instance space X, and each feature \(y_i\) is in some label set Y (in this case assuming that \(Y = \{-1, +1\}\)).This method repeatedly invokes a particular weak or base learning algorithm through a given number of rounds \(t = 1, . . . , T\). One of the key ideas in the algorithm is to maintain a distribution or collection of weights over the training set. The weight of this distribution on training samples i on round t will be denoted by \(D_t(i)\). Initially, all weights are equal, but at every round, the weights of misclassified samples are increased so that the weak learner can concentrate on hard samples in the training data. The responsibility for finding a weak hypothesis \(h_t : X \rightarrow \{-1, +1\}\) useful under the distribution \(D_t\) still lies with the weak learner [37].
For a binary classification problem with a dataset containing m samples, denoted as \(\{(x_1, y_1), (x_2, y_2), ..., (x_m, y_m)\}\), where \(x_i\) represents the feature vector and \(y_i\) denotes the corresponding binary class label (\(y_i \in \{-1, +1\}\)), AdaBoost algorithm can be represented as follows:
Initialize sample weights \(D_t(i) =\frac{1}{m}\) for \(i = 1, 2, . . . , m\).
For \(t = 1, 2, ..., T\), where T is the number of boosting iterations:
Gradient boosting
Gradient boosting is a boosted algorithm used to solve classification and regression problems [38]. The prediction model produced by gradient boosting takes the form of a combination of weak learners, often referred to as decision trees. This stage-wise modeling approach that underlies other boosting techniques also applies to it, whereas these are further generalized by enabling optimization over any differentiable loss function [39]. In gradient boosting, a new decision tree is learned at each stage to rectify errors committed by the existing trees. Gradient boosting as a non-linear method outperforms linear models [40] when there are high-order relationships in the data. Moreover, it has surpassed other machine learning algorithms in various studies [41]. Its potential was described in recent works in the medical field [40, 42,43,44]. The gradient boosting algorithm, was originally proposed by [45] and it is represented as follows:
XGBoost
XGBoost or eXtreme Gradient Boosting [41] is a decision tree ensemble that depends on gradient boosting to be highly scalable. XGboost is built similarly to Gradient Boosting as an objective function is expanded additively through the minimization of the loss function. It is used for supervised learning tasks, such as regression and classification [46]. XGBoost builds a predictive model by combining the predictions of multiple individual models, often decision trees, in an iterative manner [47].
The algorithm works by sequentially adding weak learners to the ensemble, with each new learner focusing on correcting the errors made by the existing ones. It uses a gradient descent optimization technique to minimize a predefined loss function during training [48, 49]. To begin with, a tree ensemble method of classification and regression trees (CARTs) is utilized whereby each CART consists of \(K_{E}^{i} \mid i \in 1 \ldots K\) nodes. The total prediction scores at a leaf node \(f_{k}\) for each tree \(k^{\text{ th } }\) are used to calculate the final prediction output of class label \(\hat{y}_{i}\). This is expressed in Eq. (6).
$$\begin{aligned} \hat{y}_{i}=\varphi \left( x_{i}\right) =\sum \limits _{k=1}^{K} f_{k}\left( x_{i}\right) , \quad f_{k} \in F \end{aligned}$$
(6)
where \(x_{{i}}\) stands for training set whereas F denotes the set of all K scores for all CARTs. Afterwards, regularization step enhances the outcomes as shown by Eq. (7).
$$\begin{aligned} \mathcal {L}(\varphi )=\sum \limits _{i} \ell \left( \hat{y}_{i}, y_{i}\right) +\sum \limits _{k} \Omega \left( f_{k}\right) \end{aligned}$$
(7)
In this case, \(\ell\) represents the differentiable loss function, which is determined through finding out the error difference between the target \(y_j\) and the predicted class labels \(\hat{y}\)’s. Furthermore, there is also a design element that penalizes \(\Omega\), to make sure that models do not suffer from over-fitting complexities. Finally, there is an Eq. (8) that can be used to compute the values of the penalty function.
$$\begin{aligned} \Omega (f)=\gamma T+\frac{1}{2} \lambda \sum \limits _{j=1}^{T} w_j^2 \end{aligned}$$
(8)
where \(\gamma\) and \(\lambda\) are parameters that can be modified to control the level of regularization. The number of leaves in the tree is represented by T, while w is a set of weights corresponding to the leaves.
The Gradient Boosting (GB) is then used to efficiently solve the classification problem with loss function and extended by second-order Taylor expansion. The constant term will be removed in order to simplify the objective at step t as calculated in Eq. (9).
$$\begin{aligned} \tilde{\varvec{L}}^{(t)} & = \sum \limits _{i=1}^{n}\left[ g_{i} f_{t}\left( x_{i}\right) +\frac{1}{2} h_{i} f_{t}^{2}\left( x_{i}\right) \right] +\Omega \left( f_{t}\right) \nonumber \\ & = \sum \limits _{i=1}^{n}\left[ g_{i} f_{t}\left( x_{i}\right) +\frac{1}{2} h_{i} f_{t}^{2}\left( x_{i}\right) \right] +\gamma {T}+\frac{1}{2} \lambda \sum \limits _{{j=1}}^{{T}} w_{{j}}^{{2}}\nonumber \\ & = \sum \limits _{j=1}^{T}\left[ \left( \sum \limits _{i \in I_j} g_i\right) w_j + \frac{1}{2}\left( \sum \limits _{i \in I_j} h_i + \lambda \right) \omega _j^2\right] + \gamma T \end{aligned}$$
(9)
where \(I_j = \left\{ i \mid q\left( x_i\right) = j \right\}\) denotes instances of leaf t and equations for first-order gradient statistics \(g_i\) and second-order gradients \(h_i\) are defined in Eqs. (10)-(11).
$$\begin{aligned} g_i=\frac{\partial \ell (\hat{y}_i^{(t-1)}, y_i )}{\partial \hat{y}_i^{(t-1)}} \end{aligned}$$
(10)
$$\begin{aligned} h_i=\frac{\partial ^2 \ell (\hat{y}_i^{t-1}, y_i)}{\partial (\hat{y}_i^{t-1})^2} \end{aligned}$$
(11)
Thereafter the optimal weight \(\varvec{w}_{j}^{*}\) of leaf j can be calculated using Eq. (12).
$$\begin{aligned} \varvec{w}_{j}^{*}=\frac{\sum \nolimits _{i \in I j} g_{i}}{\sum \nolimits _{i \in I j} h_{i}+\lambda } \end{aligned}$$
(12)
Equation (13) then allows for the calculation of a function q to use as a scoring function that measures the quality of tree structure by giving it a given tree structure \(q(x_i)\).
$$\begin{aligned} \tilde{\mathcal {L}}^{(t)}(q)=-\frac{1}{2} \sum \limits _{j=1}^T \frac{\left( \sum \nolimits _{i \in I j} g_{i}\right) ^{2}}{\sum \nolimits _{i \in I j} h_{i}+\lambda }+\gamma T \end{aligned}$$
(13)
This function can be simplified by using the Taylor expansion as shown in Eq. (14) , and a formula is derived for loss reduction after the tree split from the given node:
$$\begin{aligned} \mathcal {L}_{\text {split}}=\frac{1}{2}\left[ \frac{\left( \sum \nolimits _{i \in I_{L}} g_{i}\right) ^{2}}{\sum \nolimits _{i \in I_{L}} h_{i}+\lambda }+\frac{\left( \sum \nolimits _{i \in I_{R}} g_{i}\right) ^{2}}{\sum \nolimits _{i \in I_{R}} h_{i}+\lambda }+\frac{\left( \sum \nolimits _{i \in I} g_i\right) ^{2}}{\sum \nolimits _{i \in I} h_i + \lambda }\right] - \gamma \end{aligned}$$
(14)
where I is a subset of the available observations in the current node i.e \(I = I_R \cup I_L\) and \(I_{L}\), \(I_{R}\) are subsets of the available observations in the left and right nodes after the split.
CatBoost
The CatBoost algorithm, derived from “Category Boosting”, has been widely used for its impressive handling of categorical data, which is why it makes a good choice for health data tasks that mostly involve a combination of numerical and categorical features [50]. CatBoost is an implementation of gradient boosting, which makes use of binary decision trees as base predictors. CatBoost’s ability to natively handle categorical data as well as its regularized nature that guards against overfitting positions it uniquely in the health prediction setting where feature interactions can be complex and non-linear.
Consider data consisting of samples \(D=\left\{ \left( X_{j}, y_{j}\right) \right\} _{j=1, \ldots , m}\), where \(X_{j}=\left( x_{j}^{1}, x_{j}^{2}, \ldots , x_{j}^{n}\right)\) is a vector of n features and response feature \(y_{j} \in \mathbb {R}\); the response may be encoded either numerically (0 or 1) or categorically (i.e., yes-no). The pairs \(\left( X_{j}, y_{j}\right)\) are identically and independently distributed according to an unknown distribution p(.,.). Therefore given in (15), the objective of this learning task is to train a function \(H: \mathbb {R}^{n} \rightarrow \mathbb {R}\),
$$\begin{aligned} \mathcal {L}(H) := \mathbb {E}[L(y, H(X))] \end{aligned}$$
(15)
where (X, y) is test set drawn from training data D and \(L(., \cdot )\) represents any smooth loss function. Gradient boosting [51] is carried out in a greedy manner by repeatedly constructing approximations \(H^{t}: \mathbb {R}^{m} \rightarrow \mathbb {R}, t=\) \(0,1, \ldots\). The new approximation \(H^{t}\) with respect to the previous approximation can be derived by means of an addition process such that \(H^{t}=\ H^{t-1}+\alpha g^{t}\), where \(\alpha\) denotes the step size and \(g^{t}: \mathbb {R}^{n} \rightarrow \mathbb {R}\) is a base predictor chosen from a set of functions G that aims at minimizing the expected loss defined in (16):
$$\begin{aligned} g^{t} & = \arg \underset{g \in G}{\min} \mathcal {L}\left( H^{t-1}+g\right) \nonumber \\ & = \arg \underset{g \in G}{\min}\mathbb {E} L\left( y, H^{t-1}(X)+g(X)\right) . \end{aligned}$$
(16)
The minimization problem is typically solved either using Newton’s method via second-order approximation of the function \(\mathcal L (H^{{( t - 1 )}} + g^{{( t )}} )\) at \(H^{( t - 1 )}\) or taking ( negative ) gradient steps. Either of these functions is gradient descent [45, 52].
In the last section, we showed the mathematical representation of the techniques that were used in this study. This section intends to give a description of our datasets, analytics on data, model fit, and model prediction and comparisons. To ensure reproducibility, all analyses were performed using Python 3.9.1. This software package has various great libraries, including Pandas for data handling in general, Matplotlib and Seaborn for visualizing, Scikit-learn [53] for pre-processing, data splitting, model building and evaluation as well as explainability with LIME and Permutation Feature Importance.
From the different studies that have used deep learning models, it is evident that ensemble methods effectively minimize false positives and false negatives, increasing confidence in diagnosing malaria. These models are particularly useful in addressing the challenges of skewed variable distributions in large, imbalanced datasets. In such cases, smaller attributes can be overshadowed, leading to misclassification and significant prediction errors. However, machine learning techniques refine these predictions, helping to uncover hidden patterns in the data. These insights are crucial for public health interventions aimed at controlling malaria. Examples include accurate malaria outbreak prediction models [54, 55], the complexities of parasite transmission [56], identifying areas for targeted disinfection [57] and predicting immune system resilience to parasite incursions [56].
This study employed a comprehensive malaria dataset, collected over a four-week period at a medical center in Nigeria, to investigate and model malaria-related symptoms. The dataset comprises detailed records of 337 patients who presented with symptoms indicative of malaria, providing a rich source of information for analysis. The data is sourced from a peer-reviewed research article, accessible at Malaria Dataset, ensuring its credibility and relevance for scientific inquiry. The patient cohort spans a wide age range, from 3 to 77 years, with an average age of 35.4 years (SD = 14.7). Gender distribution within the dataset shows 180 females and 157 males, indicating a slight gender imbalance. This demographic diversity supports a nuanced analysis of malaria’s impact across different age groups and genders. An exploratory data analysis revealed a class imbalance in the target variable, where 65.6% of the patients were not diagnosed with malaria, while 34.4% were confirmed to have the disease. Such an imbalance in the data is a critical consideration, as it can influence the performance of predictive models. Addressing this imbalance is necessary to develop a model that provides accurate and unbiased predictions.
To identify the most relevant features for analysis, a systematic feature selection process was conducted. This resulted in a final set of 16 features, encompassing both categorical and numerical variables, in addition to the target variable, severe_malaria. The target variable distinguishes between the presence (1) and absence (0) of severe malaria. A comprehensive summary of these features is presented in Table 1. Importantly, the dataset is complete, with no missing values, which enhances its reliability and suitability for building robust predictive models. This completeness, combined with its diverse demographic and categorical information, makes the dataset a valuable resource for malaria research and modeling efforts.
In this study, Spearman Rank Correlation Coefficient analysis was applied to the malaria dataset to assess the relationship between features and the target variable. Figure 2 illustrates a correlation plot of the dataset, where variables with correlation coefficients close to 1 and −1 indicate strong positive and negative correlations, respectively. A threshold of 0.05 was set, and features with correlation coefficients below this threshold were eliminated which resulted in the removal of ’sex’ from the features. As a result, 16 features were retained for further analysis [58]. In this study, we standardized our data to ensure the data was on the same scale and for consistent results across the models used.
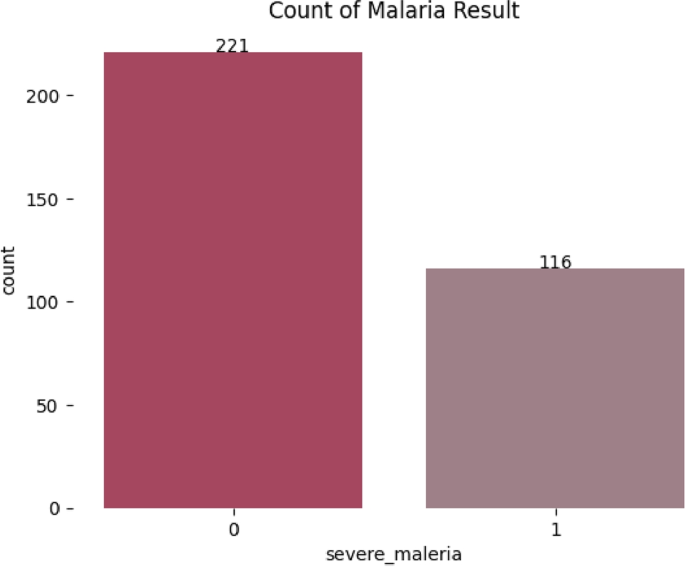
Handling Class Imbalance: One of the primary preparation steps in this work was to manage the imbalance in the dataset, which, if not managed properly, could lead to bias in model training because machine learning models tend to favor classes with the most representation. The imbalance ratio of the Malaria dataset before balancing was 1:2, meaning that for every malaria patient, there were approximately two non-malaria patients. The highly imbalanced nature of the data, therefore, made it imperative for balancing to be carried out. Figure 3 illustrates the class distribution for the Malaria dataset. Subsequently, Fig. 4 shows the class distribution after applying oversampling to balance the Malaria data set. In this study, an oversampling technique was used to balance our classes on the data used to train our models Malaria dataset. We balanced the train set instead of the entire dataset to reduce the chances of overfitting. Other methods, such as synthetic data generation, were not considered because the dataset involved sensitive medical data, where synthetic data generation could introduce risks of inaccuracies or distortions that might compromise the integrity of the study.
In this section, the results of the models used in our study are presented. A number of performance evaluation metrics were employed in order to determine how effective the models were, including accuracy, balanced accuracy, Matthew Correlation Coefficient (MCC), precision, and Area Under the Receiver Operating Characteristic (AUC-ROC) curve score. The Malaria dataset used in this study was divided into a 70:30 ratio, with 70% used for training and 30% used for testing. The following confusion matrices were obtained from the five models trained on the imbalanced dataset for the Malaria dataset.
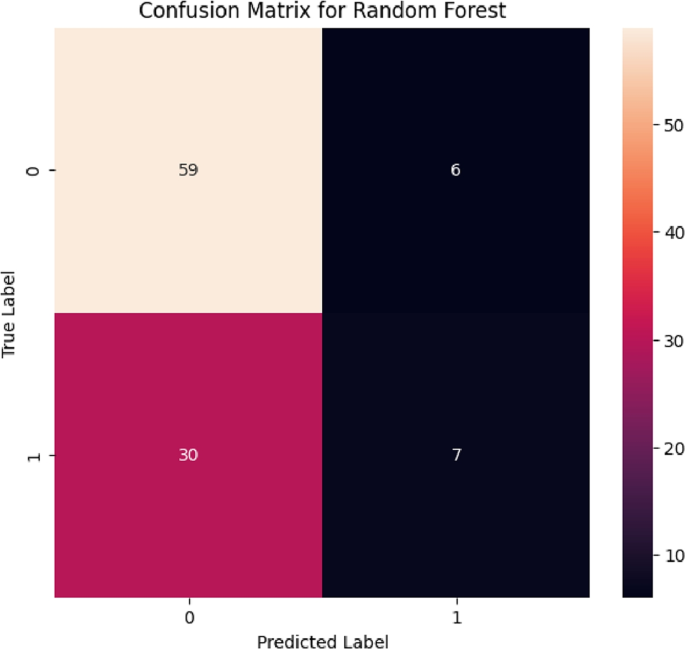
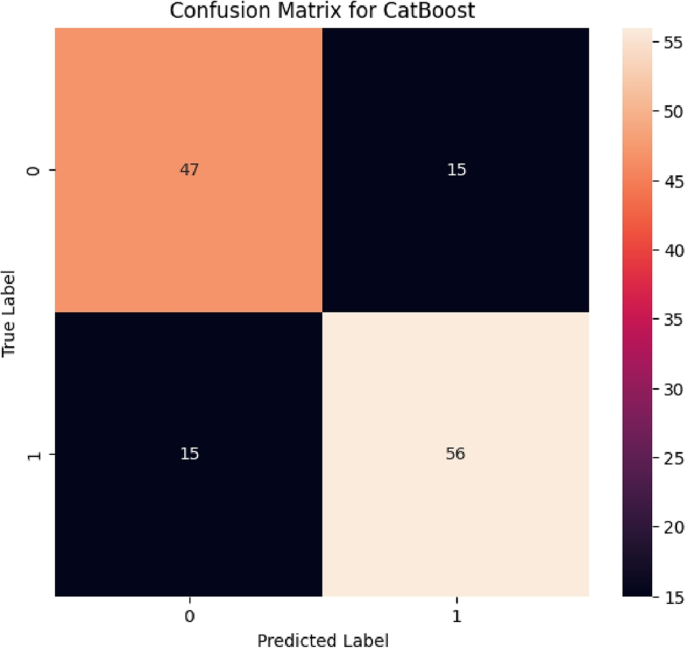
From the confusion matrices generated in Figs. 5, 6, 7, 8, and 9, the study can observe the impact of data imbalance and the necessity of incorporating balancing techniques in the study. It is evident that all the models struggle to correctly identify the true negative (TN) classes effectively, especially out of the 37 correct negative classes in the test dataset. The performance metrics of these models can be seen in Table 2.
While the Random Forest model achieves the highest accuracy score (64.7%), it struggles with balanced accuracy (54.8%) and MCC (0.140), indicating challenges in correctly identifying true negatives. CatBoost follows closely with slightly lower accuracy (63.7%) but exhibits a higher balanced accuracy (55.2%) and MCC (0.132), showcasing better overall performance in handling the imbalanced dataset. Gradient Boost and AdaBoost models also face difficulties in balanced accuracy and MCC, indicating similar struggles in TN identification. XGBoost shows lower overall performance metrics, with the lowest accuracy (58.8%) and MCC (0.078) among the models, although it exhibits relatively higher recall and F1 scores, suggesting better identification of positive instances despite struggling with overall accuracy. The overall analysis of the ensemble machine learning models indicates that evaluating multiple metrics beyond just accuracy is crucial, especially when dealing with imbalanced datasets. While accuracy provides a general measure of performance, metrics like balanced accuracy, Matthews Correlation Coefficient (MCC), recall, and F1 scores offer a deeper insight into how well the models handle different classes. The primary challenge observed across most models was the difficulty in correctly identifying true negatives, underscoring the need to address class imbalance during model training and evaluation.
The findings here suggest that although the Random Forest model achieved the highest accuracy, CatBoost displayed a more balanced performance across all classes, making it potentially more suitable for real-world malaria diagnosis applications. This study highlights the importance of using a comprehensive set of evaluation metrics to fully assess model performance, particularly in critical fields such as medical diagnostics where both false positives and false negatives can have significant consequences.
From Figs. 10, 11, 12, 13, and 14, there were notable improvements in the true positive (TP) and true negative (TN) identification for all the ensemble machine learning models in the Malaria dataset after applying oversampling technique to address class imbalance. Specifically, both the Random Forest (RF) and CatBoost models showed enhanced TP and TN rates, indicating improved accuracy in identifying both malaria and non-malaria cases. Conversely, while the XGBoost model demonstrated improved TP rates, there was a slight increase in false positives (FP), leading to a lower TN rate. AdaBoost and GradientBoost models also exhibited mixed results in TP and TN identification, highlighting the effects of oversampling on the model’s performances as displayed in Table 3.
After implementing oversampling techniques to handle a class imbalance in the Malaria dataset, significant improvements were observed in the performance metrics of various machine-learning models. Both the Random Forest and CatBoost models exhibited substantial increases in accuracy scores, reaching 76.7%, along with improved ROC-AUC scores of 0.853 and 0.821, respectively. These enhancements also translated to higher Matthews correlation coefficient (MCC), balanced accuracy, Cohen’s Kappa coefficient, precision, recall, and F1 scores, reflecting better overall predictive capabilities in malaria diagnosis. The Gradient Boost and XGBoost models also showed notable improvements across most metrics, although slightly lower than Random Forest and CatBoost. However, the AdaBoost model, while showing some improvements, post-oversampling, still lagged behind significantly in accuracy and other performance metrics compared to the other models.
The ROC curve is shown in Fig. 15.
Using oversampling to handle class imbalance in the Malaria dataset, Random Forest (RF) and CatBoost stand out as the top-performing models. RF achieves an AUC of 0.87, highlighting its robust ability to distinguish between positive and negative instances accurately. CatBoost also excels with an impressive AUC of 0.84, showcasing its effectiveness in accurate classification. Gradient Boost and XGBoost show notable improvements with AUC values of 0.76 and 0.81, respectively, while AdaBoost achieves an improved AUC of 0.66.
After hyperparameter tuning for the malaria prediction as shown in Table 4, Random Forest emerged as the top-performing model, demonstrating strong predictive capabilities across various evaluation metrics. With an accuracy score of 0.819, Random Forest effectively distinguishes between malaria-positive and negative cases. Its ROC AUC score of 0.870 indicates that the model performs well in separating the two classes, showcasing its ability to rank predictions with high confidence. The model’s Matthew’s Correlation Coefficient (MCC) of 0.637 reflects a good balance in predicting both classes correctly, making it suitable for dealing with the class imbalance often present in malaria datasets.
Additionally, the balanced accuracy of 0.819 indicates that Random Forest is robust in handling class distributions, providing consistent performance for both malaria-positive and negative instances. Its Cohen’s Kappa score of 0.637 further confirms the model’s reliability, reflecting a substantial agreement between the predicted and actual classifications beyond random chance. Both precision and recall at 0.831 demonstrate that Random Forest strikes an excellent balance between identifying true malaria cases (high recall) and minimizing false positives (high precision). This balance is crucial in healthcare settings where the cost of mis-classification can be high, especially when predicting a serious condition like malaria. In comparison, AdaBoost performed the worst, with a low accuracy of 0.579 and an MCC of only 0.156, showing weak predictive power and struggles with classifying malaria cases. Gradient Boost and XGBoost performed moderately, with accuracy scores of 0.729 and 0.692, respectively. These models, while decent, lacked the precision and robustness shown by Random Forest. Their lower MCC and Cohen’s Kappa scores indicate that they did not handle class distributions as well, leading to more errors in classification.
Random Forest (RF) and CatBoost have shown excellent performance, as shown in Tables 3 and 4. This indicates their strength in dealing with health data classification. Random Forest can address health data with a large number of features, which enables it to identify complex relationships within medical datasets more efficiently. Being an ensemble model that combines many decision trees, it prevents overfitting and enhances generalization, useful in healthcare where accuracy is required [32]. On the other hand, what makes CatBoost so effective is its capability to handle categorical features as well as built-in protection against overfitting [50]. This feature is critical in malaria diagnostics, where categorical data such as patient demographics and symptom presence play a significant role. Its gradient-boosting framework optimizes learning from previous iterations, focusing on difficult examples and reducing bias, which proves advantageous in medical datasets characterized by imbalanced classes and subtle variation patterns. This focus is reflected in metrics like AUC-ROC and F1 score, which are crucial for imbalanced data as they consider both positive class recall and overall accuracy. Compared to other ensemble models, Random Forest and CatBoost consistently outperform them in accuracy, precision, recall, F1 scores, and AUC-ROC. This shows that they are very effective in finding useful patterns from complicated health data, especially when imbalanced class distributions exist. They are also very important for predictive modeling in healthcare. In the light of this, they can be used for early diagnosis and optimization of treatment plans, among others, leading to patient outcome predictions.
To obtain explanations of a model’s prediction using the LIME package in Python, we compile a list of attributes used to train the model, define class labels (e.g., Severe Malaria and no Malaria for the Malaria prediction dataset), and create a function that provides probabilities for each feature. The function is then fed in as an array. All components are sent to the LIME explainer object. After inputting an observation, the explainer predicts and provides insights into how each feature contributes to the classes presented. In this study, we utilize the LIME method to analyze the performance of the Random Forest and CatBoost model.
Figure 16 shows LIME analysis results for interpreting the random forest model’s predictions for Severe Malaria at a specific instance. The model predicts a 0.92 probability that this instance is likely to have severe malaria. The key indicators identified are headache, coca-cola urine, prostration, age, convulsion, diarrhea, and hyperpyrexia, each contributing varying levels of significance to the prediction. Headache emerges as the most important feature with an importance score of 0.10, followed closely by coca-cola urine and prostration, each contributing 0.06, and age with a contribution of 0.05. Conversely, the model predicts a 0.08 probability that this instance is unlikely to have malaria. The model considers symptoms like rigor, cold, and vomiting, which have minimal importance in the model’s decision-making process (probabilities \(\le 0.03\)). What this means is that sometimes certain signs strongly affect the predictions made by the system, hence illuminating various reasons behind diagnosis or non-diagnosis of malaria in different cases.
CatBoost model exhibits a slightly lower confidence level at 0.85 for severe malaria prediction and 0.15 towards predicting no malaria as shown in Fig. 17. Key factors contributing to the CatBoost model’s malaria prediction encompass symptoms like headache, coca-cola urine, prostration, age, convulsion, diarrhea, and hyperpyrexia. Notably, headache holds the highest importance at 0.13, trailed by age, prostration, and Coca-Cola urine at 0.09 each. Additionally, convulsion, diarrhea, and hyperpyrexia significantly contribute to predictions with importance values of 0.07, 0.05, and 0.04, respectively. On the other hand, features such as rigor, cold, and vomiting suggest non-malaria prediction, with importance values of 0.06, 0.04, and 0.03, respectively. The key factors identified by LIME for the Random Forest and CatBoost models include headache, coca-cola urine, prostration, age, convulsion, diarrhea, and hyperpyrexia. These factors align well with clinical observations, as symptoms like prostration and hyperpyrexia are indicative of severe malaria and high parasitic loads. Coca-cola urine, a sign of hemoglobinuria, reflects severe red blood cell destruction, often associated with Plasmodium falciparum infections. Age, a critical predictor, corresponds to documented variations in immunity and disease severity across different age groups.
SHAP (SHapley Additive exPlanations) values are a crucial tool for interpreting machine learning models, especially in medical contexts like malaria prediction. By breaking down the contributions of each feature to the model’s output, SHAP helps clinicians and data scientists understand which factors most strongly influence the prediction of malaria risk. This interpretability allows for greater trust in model decisions, especially in high-stakes environments like healthcare.
From Fig. 18, which shows the SHAP summary plot, we can observe how individual features related to malaria symptoms influence the model’s predictions. Age emerges as a highly influential factor, with older individuals (indicated by red points) contributing positively to the malaria prediction. This could be due to age-related or susceptibility factors, and this is also supported by previous studies such as [59] which identified age as a significant risk factor for severe Plasmodium falciparum malaria in nonimmune patients. Similarly, diarrhea and hypoglycemia have a notable spread in their SHAP values, indicating they significantly affect the likelihood of malaria prediction. For instance, higher SHAP values for diarrhea suggest that patients exhibiting this symptom are more likely to be predicted as having malaria. Other features like anemia, headache, and cold also contribute, albeit to a lesser extent. This variability in SHAP values across features allows us to see how symptoms commonly associated with malaria influence individual predictions in different ways.
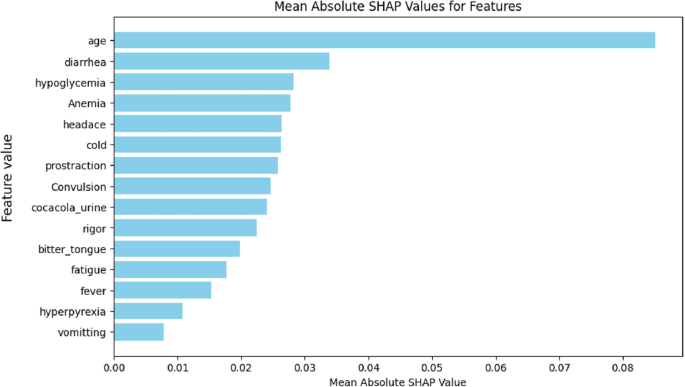
From Fig. 19, the mean absolute SHAP values help us understand the overall importance of each feature in predicting malaria. Age is the most critical feature, with the highest mean SHAP value, suggesting that it plays the most significant role in determining malaria risk. Following age, diarrhea and hypoglycemia are also prominent features, indicating that these symptoms are highly predictive of malaria. Features such as anemia and convulsion, which are commonly associated with severe malaria, show moderate importance, suggesting their role in specific prediction instances. On the other hand, features like vomiting and hyperpyrexia have relatively low SHAP values, indicating that, on average, they contribute less to the model’s predictions.
In addition to LIME, which explains individual predictions, we also used Permutation Feature Importance (PFI) to know what features are important for our machine learning models on average. By shuffling a feature’s values and thus breaking the relationship between that feature and the target variable, PFI disrupts its measures of how much this affects the model’s performance - the larger the drop in performance, the more significant that feature is for predicting with this model. LIME gives information about particular instances, while PFI shows the importance of features across the whole dataset. Such a combination allowed us to see how different aspects contribute to models’ performance.
Figure 20 shows permutation feature importance (PFI) analysis for the Random Forest model. Age emerged as the most important factor, highlighting its established association with malaria risk in younger children and older adults. The model also placed moderate importance on various symptoms for prediction, including headaches, rigors, the presence of Coca-Cola-colored urine, vomiting, diarrhea, and convulsions. Biological indicators like fever, hyperpyrexia, and potential prostration also seem to influence the model’s predictions. Hyperpyrexia, defined as a fever exceeding 39°C, reflects the body’s inflammatory response to Plasmodium falciparum infection and is associated with higher parasitic loads, highlighting its clinical relevance in severe malaria [60].
Anemia had a negligible PFI score, as shown in the red bar, warranting further exploration to understand its role in the model. Finally, some symptoms like cold, fatigue and bitter taste had lower importance scores, suggesting that the model might rely on them less. However, these features could still hold some informative value. It’s also worth noting that hypoglycemia (low blood sugar) had a very low PFI score, suggesting a weaker influence on the model’s predictions compared to other features.
Similar to the Random Forest model, permutation feature importance (PFI) analysis provided insights into feature importance for the CatBoost model as shown in Fig. 21. Here too, age emerged as the most important factor, aligning with its established role in malaria risk assessment. The model also placed moderate importance on various symptoms for prediction, such as headaches, rigors, prostration, presence of Coca-Cola-colored urine, vomiting, diarrhea, and convulsions. These symptoms likely play a significant role in the CatBoost model’s malaria prediction process.
Interestingly, anemia showed a slight increase in importance in the CatBoost model compared to Random Forest, although its PFI score remained relatively low. Biological indicators like fever and hyperpyrexia also gained weight from the CatBoost model, though potentially less than some symptoms. Finally, some symptoms like cold, fatigue and bitter taste had lower importance scores, suggesting that the model might rely on them less for prediction. Malaria, especially in its severe form, is characterized by a range of clinical symptoms that reflect the physiological impact of the disease on the body. The features in our dataset, such as age, fever, rigor, fatigue, convulsion, anemia, jaundice, and coca-cola urine are key indicators of disease progression. Severe malaria often presents with life-threatening complications such as convulsions, anemia, and hypoglycemia, which are common in cerebral malaria and severe anemia cases. For example, symptoms like jaundice (yellowing of the skin and eyes) and dark-colored urine (coca-cola urine) signal organ damage, which is critical in identifying severe malaria cases. These clinical manifestations create complex interactions between the symptoms, which our models have been designed to capture.
From a methodological perspective, Random Forest and CatBoost are particularly well-suited to handle this complexity. Random Forest excels in managing non-linear interactions among features and provides interpretable models by ranking feature importance, allowing us to determine which symptoms most strongly indicate severe malaria. For instance, it identifies critical symptom combinations like convulsion and prostration, which are hallmarks of severe cases. Similarly, CatBoost effectively handles categorical features such as symptom presence (fever, vomiting, convulsion) and continuous variables like age without requiring extensive preprocessing, leading to better performance. Its gradient boosting approach enables it to capture subtle differences in symptom severity and progression, such as distinguishing mild fever from hyperpyrexia. Together, the biological relevance of these symptoms and the methodological strengths of Random Forest and CatBoost provide a clear rationale for why these models performed best in predicting severe malaria.
Predicting medical conditions like malaria accurately is crucial in healthcare analytics, as it aids in timely diagnosis and appropriate treatment planning, thereby improving decision-making regarding patient outcomes and reducing healthcare costs. This study compared the performance of five ensemble models: Random Forest, CatBoost, Gradient Boosting, AdaBoost, and XGBoost, using a malaria dataset. The results consistently demonstrated that both Random Forest and CatBoost significantly outperformed the other ensemble models in terms of balanced accuracy, precision, recall, and F1 scores. This dominance was particularly evident after implementing data balancing techniques to address the class imbalance issues commonly encountered in healthcare data. Moreover, hyperparameter tuning played a vital role in enhancing model performance, optimizing parameters such as tree depth, learning rate, and the number of estimators. This careful tuning allowed for improved model fitting to the data, which translated into better predictive accuracy and robustness. In addition to achieving high levels of accuracy, these two methods have proven themselves capable across various evaluation measures, making them ideal tools within healthcare predictive modeling systems based on statistical methods.
Using explainable techniques like Local Interpretable Model-agnostic Explanations (LIME), SHapley Additive exPlanations (SHAP), and Permutation Feature Importance (PFI), we gained valuable insights into feature importance and model decision-making processes. With the LIME explanation approach, we were able to see how each feature influences the predicted class of a model for a given instance. SHAP provided a unified, consistent approach to interpreting individual feature contributions by quantifying their impact across all predictions, making it highly valuable for both global and local interpretability. Permutation Feature Importance helped identify the most influential features contributing to the model’s predictions, enhancing transparency and interpretability. We also found that models trained on imbalanced healthcare data can yield biased results that impact patient care. These methods helped us understand key predictive features in conditions like malaria. This transparency aids healthcare professionals in interpreting model decisions, promoting trust and informed medical actions, and ultimately improving patient outcomes and system reliability. This study has established Random Forest and CatBoost as best for malaria prediction.
This study offers several important benefits. First, the use of machine learning models in malaria diagnosis demonstrates the potential for automated and accurate predictions, which can greatly assist clinicians, especially in resource-limited settings. These models are capable of analyzing large amounts of data more efficiently than traditional diagnostic methods, making them valuable tools in detecting patterns that may not be immediately visible. The completeness of the dataset, with no missing values, enhances the reliability of the model’s predictions within the scope of the study, ensuring that the insights are based on comprehensive data.
This study has several limitations that are important to acknowledge. First, the dataset includes only 337 patients, which may impact the robustness of our analyses and limit the generalizability of the findings. A larger sample size would provide more confidence in the results and help uncover more subtle trends. Additionally, the data was gathered from a single medical center over a four-week period, which may introduce biases related to specific local practices and patient demographics. While it is a positive aspect that the dataset is complete and has no missing values, we must remain cautious of potential biases that could arise from how the data was collected. Furthermore, the short duration of data collection might not fully capture seasonal variations in malaria cases, suggesting that a longer study period could offer deeper insights into the disease’s dynamics. Another limitation is the lack of external data validation; due to limited access to external datasets during the study, we were unable to validate the model on independent data. This restricts the ability to fully assess the generalizability of the findings across different populations.
In terms of future work, another key area for improvement is the comparison of machine learning models with traditional malaria diagnostic methods. While ML models offer significant improvements in automation and predictive accuracy, traditional methods such as microscopy and rapid diagnostic tests remain the gold standard in many regions. Future research would focus on hybrid approaches that combine traditional methods with machine learning models to provide more robust and interpretable results. Additionally, future studies should aim to gather data from larger, more diverse populations over extended periods and incorporate external validation to enhance the reliability of predictive models and their applicability in real-world clinical settings.
We wish to thank the editor and anonymous reviewers of this article. Kindly note that this article did not receive any funding support from anywhere. We would appreciate your help and consideration for a complete APC waiver in this regard to enable the publication of our article in your esteemed journal. We believe that the publication of our article will attract some citations and more esteemed researchers to your journal. Thank you in anticipation!
This work did not receive any funding.
Not applicable.
Not applicable.
The authors declare no competing interests.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
Awe, O.O., Mwangi, P.N., Goudoungou, S.K. et al. Explainable AI for enhanced accuracy in malaria diagnosis using ensemble machine learning models. BMC Med Inform Decis Mak 25, 162 (2025). https://doi.org/10.1186/s12911-025-02874-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s12911-025-02874-3