Past Chapters (Early access for paying subscribers)

In 2006, the NSA hid a in the Dual EC DRBG cryptographic standard. They denied it for 8 years. The Snowden leaks proved it.

Dual Elliptic Curves, as we saw earlier, are used as secure random number generators (RNGs). The mathematical backdoor let the US government decrypt SSL internet traffic (Green 2013)1.

This is a technical deep dive for programmers. We’ll implement both the government’s original paper (SP 800-90 2006)2 and the backdoor found by Microsoft researchers (Shumow & Ferguson 2007)3.

On my home computer, it takes 2 minutes to crack 28 bytes (not bits) using the backdoor. Imagine how much internet traffic the US government could decrypt on DOD supercomputers,

The Dual EC mathematical backdoor allowed the US government to eavesdrop on internet traffic. These are some other interesting attacks leveraging insecure random number generators (RNGs):

The authors of NIST SP 800-90 (2006) introduce several pseudorandom number generator (PRNG) algorithms but devote of the paper to the Dual EC algorithm.

*In the paper, Dual EC DRBG stands for Dual Elliptic Curve Deterministic Random Bit Generator.

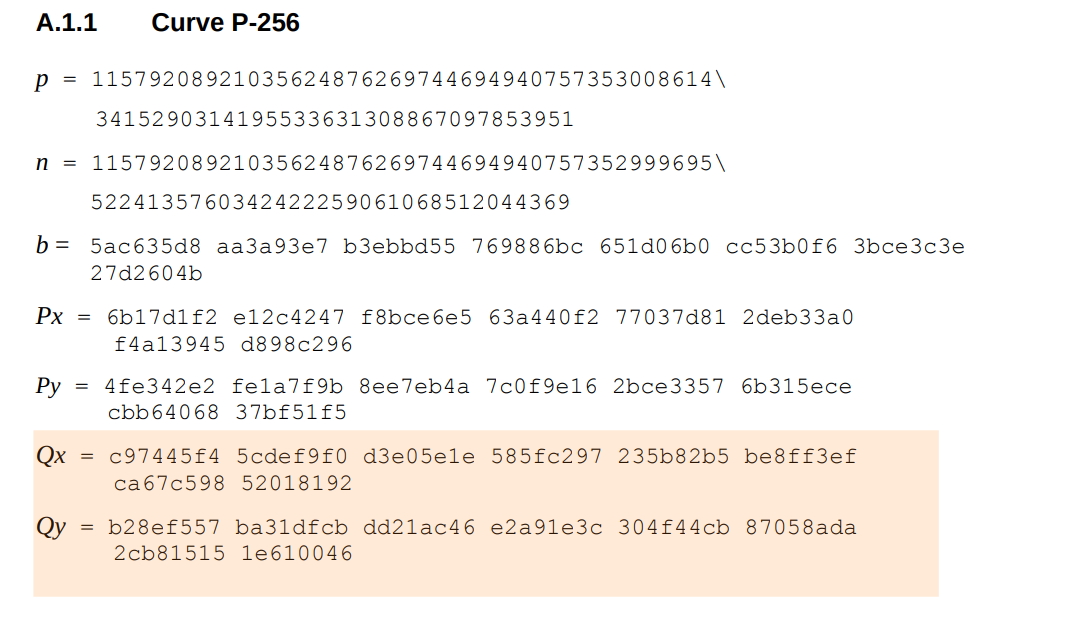
Dual EC generates random bits using elliptic curves. According to the paper, we need to use one of the NIST approved elliptic curves. I shall use P256 from the Python fastecdsa library.

Install fastecdsa using this pip command:

pip install 'fastecdsa>=1.4.1'

Then, import the library like this:

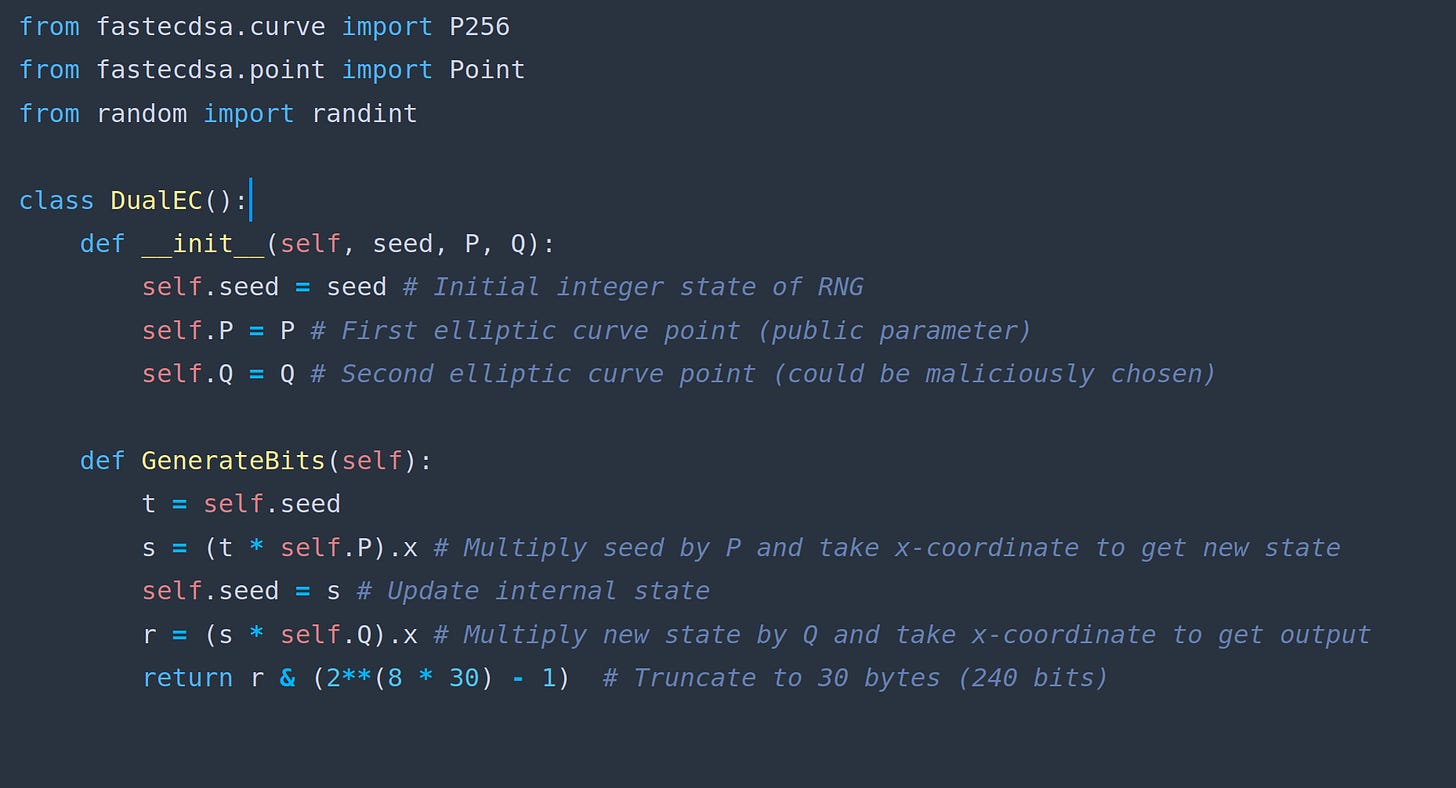
As we saw in earlier chapters, we need to define two points on our elliptic curve, and . We also need to provide an initial state for our RNG. We can put all this in a class:

class DualEC(): def __init__(self, seed, P, Q): self.seed = seed # Initial integer state of RNG self.P = P # First elliptic curve point (public parameter) self.Q = Q # Second elliptic curve point (could be maliciously chosen) 

The RNG logic is pretty simple:

We can write a function called GenerateBits to achieve our logic:

def GenerateBits(self): t = self.seed s = (t * self.P).x # Multiply seed by P and take x-coordinate to get new state self.seed = s # Update internal state r = (s * self.Q).x # Multiply new state by Q and take x-coordinate to get output return r & (2**(8 * 30) - 1) # Truncate to 30 bytes (240 bits)

By the end of this section, your DualEC class should resemble this:

According to the researchers who found the backdoor, the problem with the Dual EC algorithm is in the value. is provided as a constant in the appendix of NIST SP 800-90 (2006) but no one really knows where it came from(Schneier 2007)6.

We know what P is : the generator of the curve. BUT. What about ?

Shumow & Ferguson (2007) observed that one could easily guess a number satisfying the property of the curve:

Thus, the mathematical backdoor is the US government knowing the value of e.

In practice, it’s difficult for us to know the exact value of that satisfies the constant provided as a constant in NIST SP 800-90 (2006). Therefore, for our proof of concept, we shall use a small value that’s easy to attack.

In our implementation, we shall generate our own curve constants. We can do this by finding the modular inverse and curve exponentiation using this function:

def ModularInverse(a, m): # only works if m is prime (due to Euler's Theorem) return pow(a, m-2, m) def GenerateBackdoorConstants(): P = P256.G # set P to the curve base d = randint(2, P256.q) # pick a number random number in the field e = ModularInverse(d, P256.q) # find inverse of the number in the field Q = e * P #This is exponentiation in P256 return P, Q, d

Inside our main function, we can run this code to generate some random numbers using our constants :

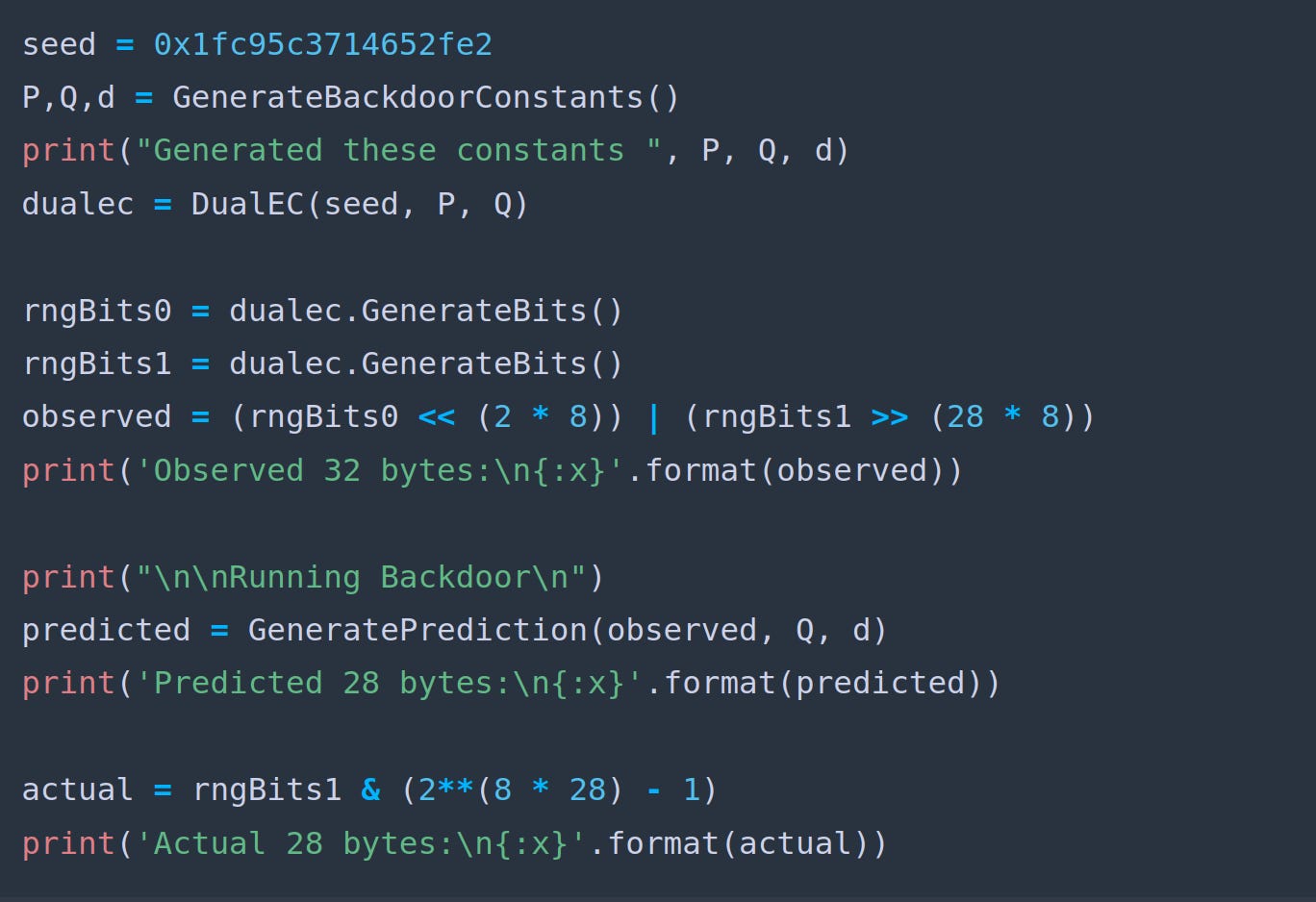
seed = 0x1fc95c3714652fe2 P,Q,d = GenerateBackdoorConstants() print("Generated these constants ", P, Q, d) dualec = DualEC(seed, P, Q) rngBits0 = dualec.GenerateBits() rngBits1 = dualec.GenerateBits() observed = (rngBits0 << (2 * 8)) | (rngBits1 >> (28 * 8)) print('Observed 32 bytes:\n{:x}'.format(observed))

We generated a somewhat random sequence in the previous section. Our mathematical backdoor allows us to predict the next number generated by our Dual EC RNG. To do this, we need to write these helper functions:

Modify your main function to this and run your backdoor:

On my computer it takes 2 minutes for the code to run. At the end, we observe that we can predict 28 bytes of RNG data in 2 minutes. Imagine how much internet traffic the US government could decrypt.

If you were coding along, here’s the gist.

Cited as

Kibicho, Murage. (June 2025). Chapter 8 : Secret Mathematical Backdoors in Cryptographic Elliptic Curves.. A Super Friendly Guide to Finite Fields for programmers. LeetArxiv. https://leetarxiv.substack.com/p/dual-ec-backdoor-coding-guide.

or

@article{Kibicho2025Chapter8:SecretMathematicalBackdoorsinCryptographic EllipticCurves., title = "Chapter 8 : Secret Mathematical Backdoors in Cryptographic Elliptic Curves..", author = "Kibicho, Murage", journal = "LeetArxiv", year = "2025", month = "April", url = "https://leetarxiv.substack.com/p/dual-ec-backdoor-coding-guide" }